使用Matplotlib和Seaborn在Python中进行数据可视化

2021年3月20日17:03:45 发表评论 996 次浏览

本文概述

有时似乎更容易遍历一组数据点并从中获取见解, 但通常此过程可能无法产生良好的结果。此过程可能会导致许多未发现的事情。此外, 现实生活中使用的大多数数据集太大, 无法手动进行任何分析。这实质上就是数据可视化的介入之处。

数据可视化是一种呈现数据的简便方法, 无论它多么复杂, 都可以借助图形表示来分析变量之间的趋势和关系。

以下是数据可视化的优点

  • 更容易表示强迫数据
  • 突出表现好的和坏的领域
  • 探索数据点之间的关系
  • 甚至识别较大数据点的数据模式

建立可视化时, 始终牢记以下几点是一个好习惯

  • 在构建可视化文件时, 确保正确使用形状, 颜色和大小
  • 使用坐标系的图/图更明显
  • 有关数据类型的适当绘图的知识使信息更加清晰
  • 标签, 标题, 图例和指针的使用将无缝信息传递给更广泛的受众

Python库

有很多python库可用于构建可视化对象, 例如matplotlib, vispy, 散景, seaborn, pygal, 叶片, 密谋, 袖扣和网络。在许多matplotlib和海生的似乎已广泛用于基础到中级的可视化。

Matplotlib

它是Python中令人惊叹的可视化库, 用于数组的2D绘图, 它是基于的多平台数据可视化库Numpy阵列, 旨在与更广泛的合作科学堆栈。它由John Hunter在2002年推出。让我们尝试了解一下的一些好处和功能matplotlib

  • 它基于快速, 高效Numpy而且更容易构建
  • 自成立以来, 开源社区已进行了许多改进, 因此也有了具有高级功能的更好的库
  • 维护良好的可视化输出以及高质量的图形吸引了很多用户
  • 基本和高级图表均可轻松构建
  • 从用户/开发人员的角度来看, 由于它具有广泛的社区支持, 因此解决问题和调试变得更加容易

海生

该图书馆最初是由斯坦福大学(Stanford University)构思和建造的, 位于matplotlib。从某种意义上说, 它具有一些风味Matpotlib从可视化的角度来看, 它比matplotlib并增加了功能。以下是它的优点

  • 内置主题有助于更好地可视化
  • 统计功能有助于更好地了解数据
  • 更好的美学和内置图
  • 有用的文档以及有效的示例

可视化的本质

根据用于绘制可视化效果的变量数量和变量类型, 可以使用不同类型的图表来理解关系。根据变量的数量, 我们可以

  • 单变量地块(仅涉及一个变量)
  • 双变量情节(需要多个变量)

一种单变量可以让连续变量了解变量的分布和分布, 而对于离散变量则可以告诉我们计数

同样, 双变量连续变量的图可以显示基本的统计数据, 例如相关性, 因为连续变量与离散变量的比较可能导致我们得出非常重要的结论, 例如了解不同类别变量的数据分布。一种双变量也可以建立两个离散变量之间的关系图。

箱形图

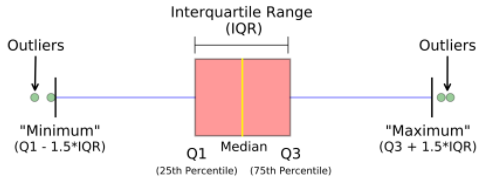
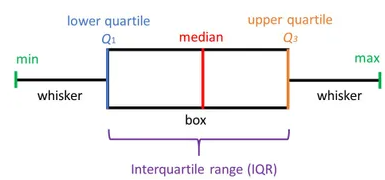
箱形图(也称为箱形和晶须图)在下图中清晰显示。在测量数据分布时, 这是非常好的视觉表示。清楚地绘制中位数, 离群值和四分位数。了解数据分布是导致更好的模型构建的另一个重要因素。如果数据有异常值, 建议使用箱形图来识别它们并采取必要的措施。

盒子和晶须图显示了数据如何分布。图表中通常包含五种信息

  1. 最小值显示在图表的最左端, 在"晶须"的末尾
  2. 第一个四分位数Q1在盒子的最左边(左晶须)
  3. 中位数在方框的中央以一条线显示
  4. 第三四分位数, Q3, 显示在框的最右边(右晶须)
  5. 最大值在盒子的最右边

从下面的图示和图表中可以看出, 可以为一个或多个变量绘制箱形图, 从而为我们的数据提供了很好的见解。

箱形图的表示。

使用Matplotlib和Seaborn在Python中进行数据可视化1

表示多元分类变量的箱形图

使用Matplotlib和Seaborn在Python中进行数据可视化2

表示多元分类变量的箱形图

Python3

# import required modules
import matplotlib as plt
import seaborn as sns
  
# Box plot and violin plot for Outcome vs BloodPressure
_, axes = plt.subplots( 1 , 2 , sharey = True , figsize = ( 10 , 4 ))
  
# box plot illutration
sns.boxplot(x = 'Outcome' , y = 'BloodPressure' , data = diabetes, ax = axes[ 0 ])
  
# violin plot illustration
sns.violinplot(x = 'Outcome' , y = 'BloodPressure' , data = diabetes, ax = axes[ 1 ])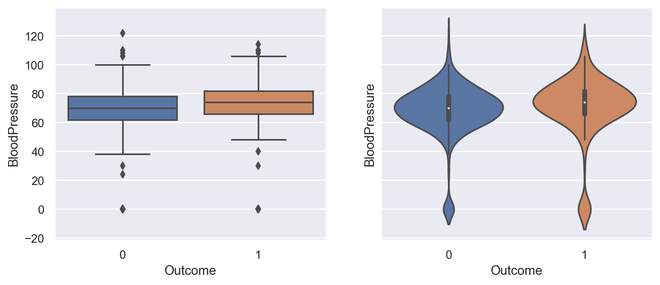
使用Matplotlib和Seaborn在Python中进行数据可视化3

箱形图和小提琴图的输出

Python3

# Box plot for all the numerical variables
sns. set (rc = { 'figure.figsize' : ( 16 , 5 )})
  
# multiple box plot illustration
sns.boxplot(data = diabetes.select_dtypes(include = 'number' ))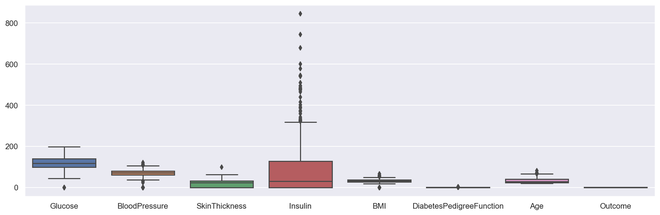
使用Matplotlib和Seaborn在Python中进行数据可视化4

输出多箱PLot

散点图

散点图或散点图是双变量在构建方式上与折线图更相似的图。线图使用X-Y轴上的线绘制连续函数, 而散布图则依赖点表示单个数据。这些图对于查看两个变量是否相关非常有用。散点图可以是2维或3维。

散点图的优点

  • 显示变量之间的相关性
  • 适用于大数据集
  • 更容易找到数据集群
  • 更好地表示每个数据点

Python3

# import module
import matpotlib.pyplot as plt
  
# scatter plot illustration
plt.scatter(diabetes[ 'DiabetesPedigreeFunction' ], diabetes[ 'BMI' ])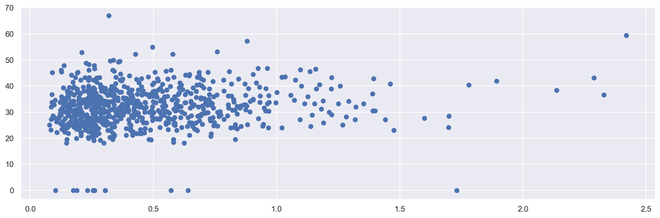
使用Matplotlib和Seaborn在Python中进行数据可视化5

输出二维散点图

Python3

# import required modules
from mpl_toolkits.mplot3d import Axes3D
  
# assign axis values
x = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ]
y = [ 5 , 6 , 2 , 3 , 13 , 4 , 1 , 2 , 4 , 8 ]
z = [ 2 , 3 , 3 , 3 , 5 , 7 , 9 , 11 , 9 , 10 ]
  
# adjust size of plot
sns. set (rc = { 'figure.figsize' : ( 8 , 5 )})
fig = plt.figure()
ax = fig.add_subplot( 111 , projection = '3d' )
ax.scatter(x, y, z, c = 'r' , marker = 'o' )
  
# assign labels
ax.set_xlabel( 'X Label' ), ax.set_ylabel( 'Y Label' ), ax.set_zlabel( 'Z Label' )
  
# display illustration
plt.show()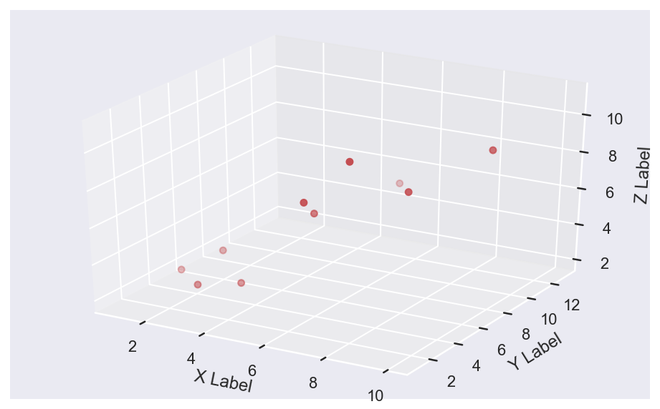
使用Matplotlib和Seaborn在Python中进行数据可视化6

输出3D散点图

直方图

直方图显示数据计数, 因此类似于条形图。直方图可以告诉我们数据分布与正态曲线的接近程度。在制定统计方法时, 拥有正态分布或接近正态分布的数据非常重要。但是, 直方图是单变量自然和条形图双变量.

条形图以类别为单位绘制实际计数条形图的高度指示该类别中的项目数, 而直方图则显示相同类别的变量垃圾桶.

箱是构建直方图时不可或缺的部分, 它们控制一个范围内的数据点。作为一个被广泛接受的选择, 我们通常将bin的大小限制为5-20, 但这完全取决于现有的数据点。

Python3

# illustrate histogram
features = [ 'BloodPressure' , 'SkinThickness' ]
diabetes[features].hist(figsize = ( 10 , 4 ))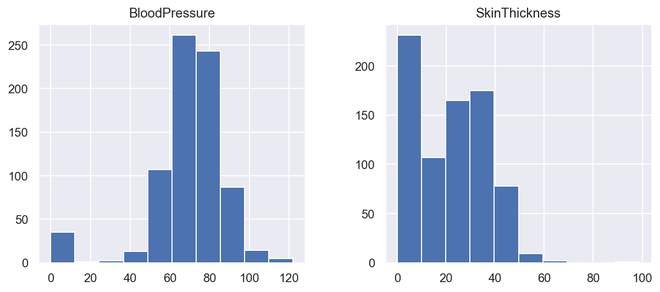
使用Matplotlib和Seaborn在Python中进行数据可视化7

输出直方图

计数图

计数图是分类变量和连续变量之间的图。在这种情况下, 连续变量是分类的出现次数或频率。从某种意义上说, 计数图可以说与直方图或条形图紧密相关。

它只是根据某种类别显示项目的出现次数。在python中, 我们可以使用海生的图书馆。海生是Python中的一个基于matplotlib并用于在视觉上吸引人的统计图。

Python3

# import required module
import seaborn as sns
  
# assign required values
_, axes = plt.subplots(nrows = 1 , ncols = 2 , figsize = ( 12 , 4 ))
  
# illustrate count plots
sns.countplot(x = 'Outcome' , data = diabetes, ax = axes[ 0 ])
sns.countplot(x = 'BloodPressure' , data = diabetes, ax = axes[ 1 ])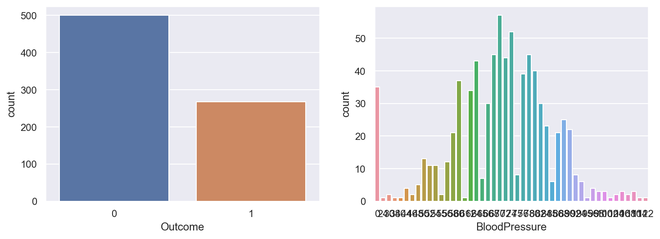
使用Matplotlib和Seaborn在Python中进行数据可视化8

输出计数图

相关图

相关图是一个多变量分析, 可以很方便地查看与数据点的关系。散点图有助于了解一个变量对另一个变量的影响。相关可以定义为一个变量对另一个变量的影响。

可以计算两个变量之间的相关性, 也可以是一个与许多相关性, 我们可以看到下图。相关性可以是正, 负或中性的, 并且相关性的数学范围是-1到1。了解相关性可能对模型构建阶段和模型输出有非常重要的影响。

Python3

# Finding and plotting the correlation for 
# the independent variables
  
# import required module
import seaborn as sns
  
# adjust plot
sns. set (rc = { 'figure.figsize' : ( 14 , 5 )})
  
# assign data
ind_var = [ 'CRIM' , 'ZN' , 'INDUS' , 'CHAS' , 'NOX' , 'RM' , 'AGE' , 'DIS' , 'RAD' , 'TAX' , 'PTRATIO' , 'B' , 'LSTAT' ]
  
# illustrate heat map.
sns.heatmap(diabetes.select_dtypes(include = 'number' ).corr(), cmap = sns.cubehelix_palette( 20 , light = 0.95 , dark = 0.15 ))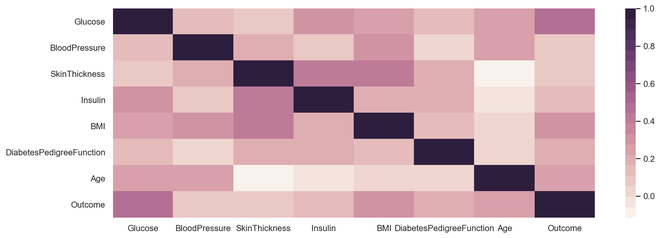
使用Matplotlib和Seaborn在Python中进行数据可视化9

输出相关图

热图

热图是多变量数据表示。热图显示中的颜色强度成为了解数据点影响的重要因素。热图更容易理解和解释。使用可视化进行数据分析时, 在绘图的帮助下传达所需的消息非常重要。

Python3

# import required module
import seaborn as sns
import numpy as np
  
# assign data
data = np.random.randn( 50 , 20 )
  
# illustrate heat map
ax = sns.heatmap(data, xticklabels = 2 , yticklabels = False )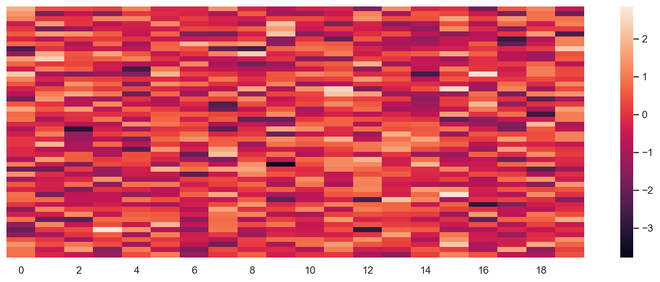
使用Matplotlib和Seaborn在Python中进行数据可视化10

输出热图

饼形图

饼图是单变量分析, 通常用于显示百分比或比例数据。变量的每个类别的百分比分布位于相应的饼图切片旁边。可以用来建立饼图的python库是matplotlib和海上的

以下是饼图的优点

  • 大数据点的可视化汇总更轻松
  • 不同类别的效果和规模很容易理解
  • 百分比点用于表示数据点中的类

Python3

# import required module
import matplotlib.pyplot as plt
  
# Creating dataset
cars = [ 'AUDI' , 'BMW' , 'FORD' , 'TESLA' , 'JAGUAR' , 'MERCEDES' ]
data = [ 23 , 17 , 35 , 29 , 12 , 41 ]
  
# Creating plot
fig = plt.figure(figsize = ( 10 , 7 ))
plt.pie(data, labels = cars)
  
# Show plot
plt.show()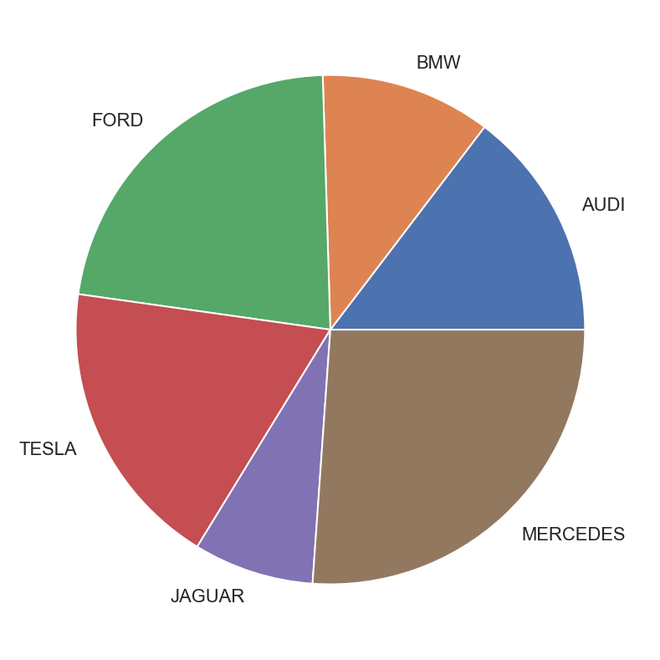
使用Matplotlib和Seaborn在Python中进行数据可视化11

输出饼图

Python3

# Import required module
import matplotlib.pyplot as plt
import numpy as np
  
# Creating dataset
cars = [ 'AUDI' , 'BMW' , 'FORD' , 'TESLA' , 'JAGUAR' , 'MERCEDES' ]
data = [ 23 , 17 , 35 , 29 , 12 , 41 ]
  
# Creating explode data
explode = ( 0.1 , 0.0 , 0.2 , 0.3 , 0.0 , 0.0 )
  
# Creating color parameters
colors = ( "orange" , "cyan" , "brown" , "grey" , "indigo" , "beige" )
  
# Wedge properties
wp = { 'linewidth' : 1 , 'edgecolor' : "green" }
  
# Creating autocpt arguments
def func(pct, allvalues):
     absolute = int (pct / 100. * np. sum (allvalues))
     return "{:.1f}%\n({:d} g)" . format (pct, absolute)
  
# Creating plot
fig, ax = plt.subplots(figsize = ( 10 , 7 ))
wedges, texts, autotexts = ax.pie(data, autopct = lambda pct: func(pct, data), explode = explode, labels = cars, shadow = True , colors = colors, startangle = 90 , wedgeprops = wp, textprops = dict (color = "magenta" ))
  
# Adding legend
ax.legend(wedges, cars, title = "Cars" , loc = "center left" , bbox_to_anchor = ( 1 , 0 , 0.5 , 1 ))
plt.setp(autotexts, size = 8 , weight = "bold" )
ax.set_title( "Customizing pie chart" )
  
# Show plot
plt.show()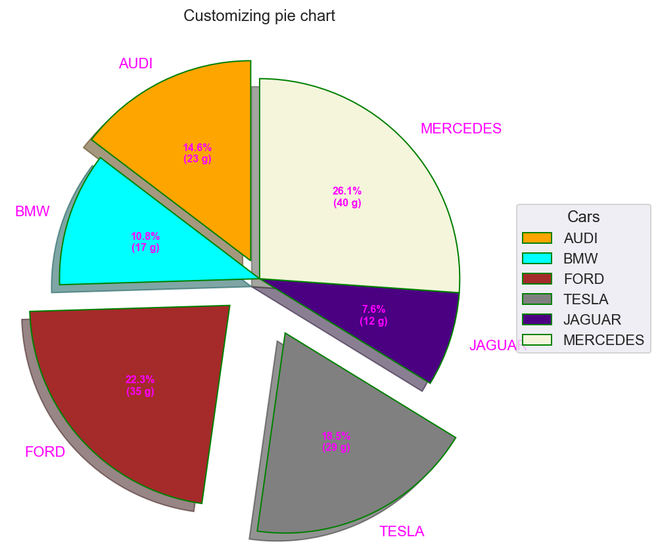
使用Matplotlib和Seaborn在Python中进行数据可视化12

输出如下

错误条

误差线可以定义为穿过图形上一个点的线, 平行于其中一个轴, 它表示该点相应坐标的不确定性或误差。这些类型的图非常易于理解和分析与目标的偏差。一旦发现错误, 就很容易对导致错误的因素进行更深入的分析。

  • 可以轻松捕获数据点与阈值的偏差
  • 轻松捕获与较大数据点集的偏差
  • 它定义了基础数据

Python3

# Import required module
import matplotlib.pyplot as plt
import numpy as np
  
# Assign axes
x = np.linspace( 0 , 5.5 , 10 )
y = 10 * np.exp( - x)
  
# Assign errors regarding each axis
xerr = np.random.random_sample( 10 )
yerr = np.random.random_sample( 10 )
  
# Adjust plot
fig, ax = plt.subplots()
ax.errorbar(x, y, xerr = xerr, yerr = yerr, fmt = '-o' )
  
# Assign labels
ax.set_xlabel( 'x-axis' ), ax.set_ylabel( 'y-axis' )
ax.set_title( 'Line plot with error bars' )
  
# Illustrate error bars
plt.show()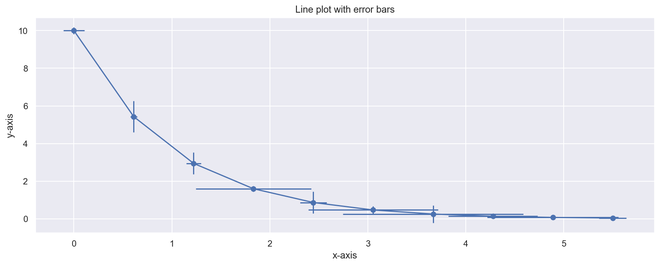
使用Matplotlib和Seaborn在Python中进行数据可视化13

输出误差图

注意怪胎！巩固你的基础Python编程基础课程和学习基础知识。

首先, 你的面试准备可通过以下方式增强你的数据结构概念：Python DS课程。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: