算法设计：如何实现二叉树删除操作？代码实现

2021年3月20日16:36:44 发表评论 947 次浏览

本文概述

给定一棵二叉树, 通过确保树从底部开始收缩来删除它的一个节点(即被删除的节点被最底部和最右边的节点替换)。这与

BST删除

。在这里, 元素之间没有任何顺序, 因此我们将其替换为last元素。

例子 ：

Delete 10 in below tree
       10
     /    \         
    20     30
Output :    
       30
     /             
    20     


Delete 20 in below tree
       10
     /    \         
    20     30
            \
            40
Output :    
       10
     /   \             
    40    30

推荐：请解决

实践

首先, 在继续解决方案之前。

算法

1.

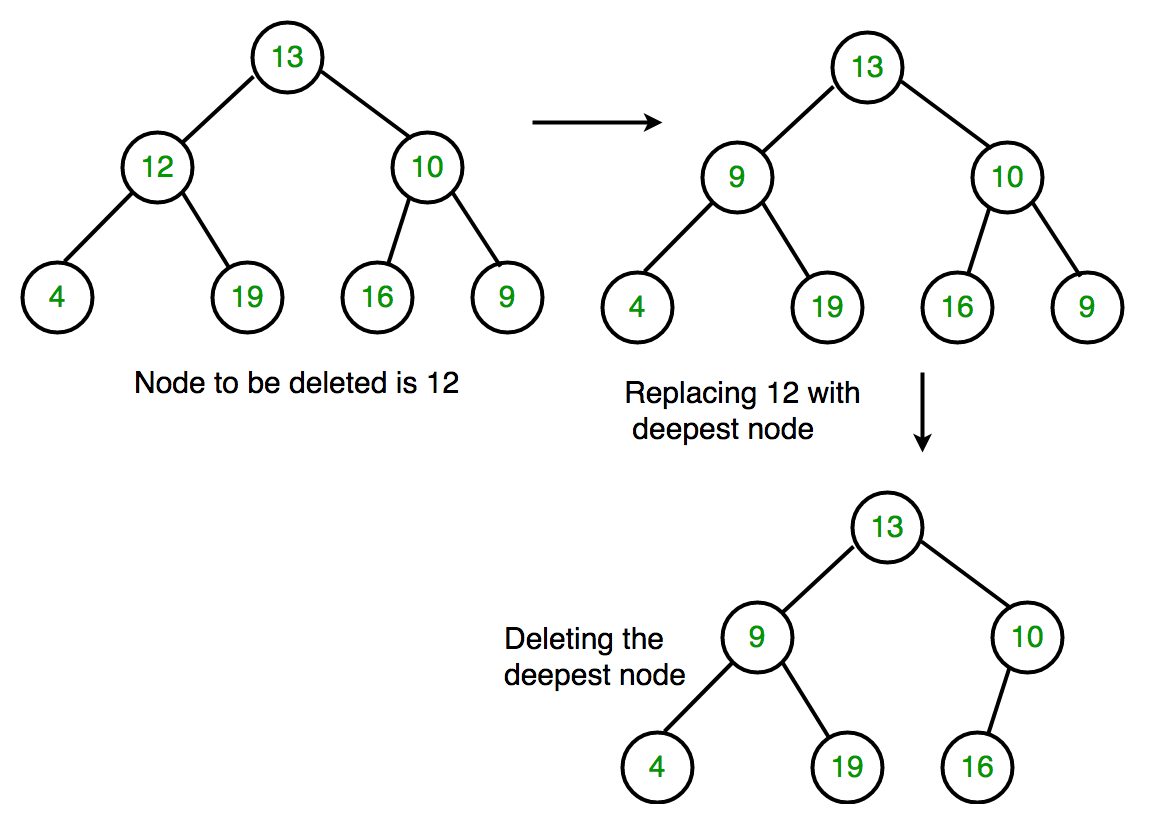
从根开始, 找到二叉树中最深和最右边的节点以及我们要删除的节点。

2.

将最深的最右边节点的数据替换为要删除的节点。

3.

然后删除最深的最右边的节点。

在二叉树中删除1

C ++

// C++ program to delete element in binary tree
#include <bits/stdc++.h>
using namespace std;
  
/* A binary tree node has key, pointer to left 
child and a pointer to right child */
struct Node {
     int key;
     struct Node *left, *right;
};
  
/* function to create a new node of tree and 
return pointer */
struct Node* newNode( int key)
{
     struct Node* temp = new Node;
     temp->key = key;
     temp->left = temp->right = NULL;
     return temp;
};
  
/* Inorder traversal of a binary tree*/
void inorder( struct Node* temp)
{
     if (!temp)
         return ;
     inorder(temp->left);
     cout << temp->key << " " ;
     inorder(temp->right);
}
  
/* function to delete the given deepest node 
(d_node) in binary tree */
void deletDeepest( struct Node* root, struct Node* d_node)
{
     queue< struct Node*> q;
     q.push(root);
  
     // Do level order traversal until last node
     struct Node* temp;
     while (!q.empty()) {
         temp = q.front();
         q.pop();
         if (temp == d_node) {
             temp = NULL;
             delete (d_node);
             return ;
         }
         if (temp->right) {
             if (temp->right == d_node) {
                 temp->right = NULL;
                 delete (d_node);
                 return ;
             }
             else
                 q.push(temp->right);
         }
  
         if (temp->left) {
             if (temp->left == d_node) {
                 temp->left = NULL;
                 delete (d_node);
                 return ;
             }
             else
                 q.push(temp->left);
         }
     }
}
  
/* function to delete element in binary tree */
Node* deletion( struct Node* root, int key)
{
     if (root == NULL)
         return NULL;
  
     if (root->left == NULL && root->right == NULL) {
         if (root->key == key)
             return NULL;
         else
             return root;
     }
  
     queue< struct Node*> q;
     q.push(root);
  
     struct Node* temp;
     struct Node* key_node = NULL;
  
     // Do level order traversal to find deepest
     // node(temp) and node to be deleted (key_node)
     while (!q.empty()) {
         temp = q.front();
         q.pop();
  
         if (temp->key == key)
             key_node = temp;
  
         if (temp->left)
             q.push(temp->left);
  
         if (temp->right)
             q.push(temp->right);
     }
  
     if (key_node != NULL) {
         int x = temp->key;
         deletDeepest(root, temp);
         key_node->key = x;
     }
     return root;
}
  
// Driver code
int main()
{
     struct Node* root = newNode(10);
     root->left = newNode(11);
     root->left->left = newNode(7);
     root->left->right = newNode(12);
     root->right = newNode(9);
     root->right->left = newNode(15);
     root->right->right = newNode(8);
  
     cout << "Inorder traversal before deletion : " ;
     inorder(root);
  
     int key = 11;
     root = deletion(root, key);
  
     cout << endl;
     cout << "Inorder traversal after deletion : " ;
     inorder(root);
  
     return 0;
}

Java

// Java program to delete element
// in binary tree 
import java.util.LinkedList; 
import java.util.Queue; 
  
class GFG{ 
      
// A binary tree node has key, pointer to 
// left child and a pointer to right child 
static class Node 
{ 
     int key; 
     Node left, right; 
      
     // Constructor 
     Node( int key)
     { 
         this .key = key; 
         left = null ; 
         right = null ; 
     } 
} 
  
static Node root; 
static Node temp = root; 
  
// Inorder traversal of a binary tree
static void inorder(Node temp) 
{ 
     if (temp == null ) 
         return ; 
  
     inorder(temp.left); 
     System.out.print(temp.key + " " ); 
     inorder(temp.right); 
} 
  
// Function to delete deepest 
// element in binary tree
static void deleteDeepest(Node root, Node delNode)
{
     Queue<Node> q = new LinkedList<Node>(); 
     q.add(root);
      
     Node temp = null ;
      
     // Do level order traversal until last node 
     while (!q.isEmpty())
     { 
         temp = q.peek(); 
         q.remove();
          
         if (temp == delNode)
         { 
             temp = null ; 
             return ; 
              
         } 
         if (temp.right!= null )
         { 
             if (temp.right == delNode)
             { 
                 temp.right = null ; 
                 return ; 
         } 
         else
             q.add(temp.right); 
     } 
  
     if (temp.left != null ) 
     { 
         if (temp.left == delNode)
         { 
             temp.left = null ; 
             return ; 
         } 
         else
             q.add(temp.left); 
     } 
} 
}
  
// Function to delete given element 
// in binary tree
static void delete(Node root, int key)
{
     if (root == null ) 
         return ; 
          
     if (root.left == null && 
        root.right == null )
     { 
         if (root.key == key) 
             return ; 
         else
             return ; 
     }
      
     Queue<Node> q = new LinkedList<Node>(); 
     q.add(root);
     Node temp = null , keyNode = null ;
      
     // Do level order traversal until
     // we find key and last node. 
     while (!q.isEmpty())
     { 
         temp = q.peek(); 
         q.remove(); 
          
         if (temp.key == key) 
             keyNode = temp; 
  
         if (temp.left != null ) 
             q.add(temp.left); 
  
         if (temp.right != null ) 
             q.add(temp.right); 
     } 
  
     if (keyNode != null )
     { 
         int x = temp.key; 
         deleteDeepest(root, temp); 
         keyNode.key = x; 
     } 
}
  
// Driver code 
public static void main(String args[]) 
{ 
     root = new Node( 10 ); 
     root.left = new Node( 11 ); 
     root.left.left = new Node( 7 );
     root.left.right = new Node( 12 );
     root.right = new Node( 9 ); 
     root.right.left = new Node( 15 ); 
     root.right.right = new Node( 8 ); 
  
     System.out.print( "Inorder traversal " +
                      "before deletion:" ); 
     inorder(root); 
  
     int key = 11 ; 
     delete(root, key); 
  
     System.out.print( "\nInorder traversal " +
                      "after deletion:" ); 
     inorder(root); 
} 
} 
  
// This code is contributed by Ravi Kant Verma

Python3

# Python3 program to illustrate deletion in a Binary Tree
   
# class to create a node with data, left child and right child.
class Node:
     def __init__( self , data):
         self .data = data
         self .left = None
         self .right = None
   
# Inorder traversal of a binary tree
def inorder(temp):
     if ( not temp):
         return
     inorder(temp.left)
     print (temp.data, end = " " )
     inorder(temp.right)
   
# function to delete the given deepest node (d_node) in binary tree 
def deleteDeepest(root, d_node):
     q = []
     q.append(root)
     while ( len (q)):
         temp = q.pop( 0 )
         if temp is d_node:
             temp = None
             return
         if temp.right:
             if temp.right is d_node:
                 temp.right = None
                 return
             else :
                 q.append(temp.right)
         if temp.left:
             if temp.left is d_node:
                 temp.left = None
                 return
             else :
                 q.append(temp.left)
   
# function to delete element in binary tree 
def deletion(root, key):
     if root = = None :
         return None
     if root.left = = None and root.right = = None :
         if root.key = = key : 
             return None
         else :
             return root
     key_node = None
     q = []
     q.append(root)
     while ( len (q)):
         temp = q.pop( 0 )
         if temp.data = = key:
             key_node = temp
         if temp.left:
             q.append(temp.left)
         if temp.right:
             q.append(temp.right)
     if key_node : 
         x = temp.data
         deleteDeepest(root, temp)
         key_node.data = x
     return root
   
# Driver code
if __name__ = = '__main__' :
     root = Node( 10 )
     root.left = Node( 11 )
     root.left.left = Node( 7 )
     root.left.right = Node( 12 )
     root.right = Node( 9 )
     root.right.left = Node( 15 )
     root.right.right = Node( 8 )
     print ( "The tree before the deletion:" )
     inorder(root)
     key = 11
     root = deletion(root, key)
     print ()
     print ( "The tree after the deletion;" )
     inorder(root)
       
# This code is contributed by Monika Anandan

输出如下

Inorder traversal before deletion : 7 11 12 10 15 9 8 
Inorder traversal after deletion : 7 8 12 10 15 9

注意：我们还可以用左, 右子节点指向NULL的任何节点替换要删除的节点数据, 但我们仅使用最深的节点来维护二叉树的余额。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: