如何实现最近最少使用（LRU）页面替换算法程序？

2021年3月19日18:54:11 发表评论 997 次浏览

本文概述

先决条件：页面替换算法

在使用分页进行内存管理的操作系统中, 需要使用页面替换算法来确定新页面进入时需要替换哪个页面。每当引用新页面且内存中不存在该新页面时, 就会发生页面错误, 并且操作系统会替换其中之一。现有页面以及新需要的页面。不同的页面替换算法建议了不同的方法来决定替换哪个页面。所有算法的目标是减少页面错误的数量。

In大号东[R兴致勃勃地üsed(LRU)算法是Greedy算法, 其中要替换的页面最近最少使用。这个想法基于参考的本地性, 不太可能使用最近最少的页面

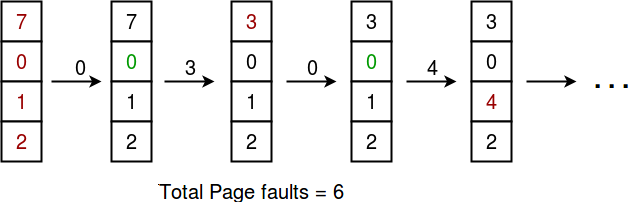
假设页面引用字符串7 0 1 2 0 3 0 4 2 3 0 3 2。最初, 我们有4个页面空白。

最初, 所有插槽都是空的, 因此当7 0 1 2分配给空插槽时->

4页错误

0已经是他们了->

0页错误。

当3出现时, 它将取代7, 因为它是最近最少使用的->

1页故障

0已在内存中, 所以->

0页故障

.

4将代替1->

1页故障

现在获取其他页面参考字符串—>

0页故障

因为它们已经在内存中可用。

LRU

给定内存容量(它可以容纳的页面数)和代表要引用的页面的字符串, 编写一个函数来查找页面错误数。

推荐：请在"实践首先, 在继续解决方案之前。

Let capacity be the number of pages that
memory can hold.  Let set be the current
set of pages in memory.

1- Start traversing the pages.
 i) If set holds less pages than capacity.
   a) Insert page into the set one by one until 
      the size  of set reaches capacity or all
      page requests are processed.
   b) Simultaneously maintain the recent occurred
      index of each page in a map called indexes.
   c) Increment page fault
 ii) Else 
   If current page is present in set, do nothing.
   Else 
     a) Find the page in the set that was least 
     recently used. We find it using index array.
     We basically need to replace the page with
     minimum index.
     b) Replace the found page with current page.
     c) Increment page faults.
     d) Update index of current page.

2. Return page faults.

以下是上述步骤的实现。

C ++

//C++ implementation of above algorithm
#include<bits/stdc++.h>
using namespace std;
  
// Function to find page faults using indexes
int pageFaults( int pages[], int n, int capacity)
{
     // To represent set of current pages. We use
     // an unordered_set so that we quickly check
     // if a page is present in set or not
     unordered_set< int > s;
  
     // To store least recently used indexes
     // of pages.
     unordered_map< int , int > indexes;
  
     // Start from initial page
     int page_faults = 0;
     for ( int i=0; i<n; i++)
     {
         // Check if the set can hold more pages
         if (s.size() < capacity)
         {
             // Insert it into set if not present
             // already which represents page fault
             if (s.find(pages[i])==s.end())
             {
                 s.insert(pages[i]);
  
                 // increment page fault
                 page_faults++;
             }
  
             // Store the recently used index of
             // each page
             indexes[pages[i]] = i;
         }
  
         // If the set is full then need to perform lru
         // i.e. remove the least recently used page
         // and insert the current page
         else
         {
             // Check if current page is not already
             // present in the set
             if (s.find(pages[i]) == s.end())
             {
                 // Find the least recently used pages
                 // that is present in the set
                 int lru = INT_MAX, val;
                 for ( auto it=s.begin(); it!=s.end(); it++)
                 {
                     if (indexes[*it] < lru)
                     {
                         lru = indexes[*it];
                         val = *it;
                     }
                 }
  
                 // Remove the indexes page
                 s.erase(val);
  
                 // insert the current page
                 s.insert(pages[i]);
  
                 // Increment page faults
                 page_faults++;
             }
  
             // Update the current page index
             indexes[pages[i]] = i;
         }
     }
  
     return page_faults;
}
  
// Driver code
int main()
{
     int pages[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2};
     int n = sizeof (pages)/ sizeof (pages[0]);
     int capacity = 4;
     cout << pageFaults(pages, n, capacity);
     return 0;
}

Java

// Java implementation of above algorithm
  
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
  
class Test
{
     // Method to find page faults using indexes
     static int pageFaults( int pages[], int n, int capacity)
     {
         // To represent set of current pages. We use
         // an unordered_set so that we quickly check
         // if a page is present in set or not
         HashSet<Integer> s = new HashSet<>(capacity);
       
         // To store least recently used indexes
         // of pages.
         HashMap<Integer, Integer> indexes = new HashMap<>();
       
         // Start from initial page
         int page_faults = 0 ;
         for ( int i= 0 ; i<n; i++)
         {
             // Check if the set can hold more pages
             if (s.size() < capacity)
             {
                 // Insert it into set if not present
                 // already which represents page fault
                 if (!s.contains(pages[i]))
                 {
                     s.add(pages[i]);
       
                     // increment page fault
                     page_faults++;
                 }
       
                 // Store the recently used index of
                 // each page
                 indexes.put(pages[i], i);
             }
       
             // If the set is full then need to perform lru
             // i.e. remove the least recently used page
             // and insert the current page
             else
             {
                 // Check if current page is not already
                 // present in the set
                 if (!s.contains(pages[i]))
                 {
                     // Find the least recently used pages
                     // that is present in the set
                     int lru = Integer.MAX_VALUE, val=Integer.MIN_VALUE;
                      
                     Iterator<Integer> itr = s.iterator();
                      
                     while (itr.hasNext()) {
                         int temp = itr.next();
                         if (indexes.get(temp) < lru)
                         {
                             lru = indexes.get(temp);
                             val = temp;
                         }
                     }
                  
                     // Remove the indexes page
                     s.remove(val);
                    //remove lru from hashmap
                    indexes.remove(val);
                     // insert the current page
                     s.add(pages[i]);
       
                     // Increment page faults
                     page_faults++;
                 }
       
                 // Update the current page index
                 indexes.put(pages[i], i);
             }
         }
       
         return page_faults;
     }
      
     // Driver method
     public static void main(String args[])
     {
         int pages[] = { 7 , 0 , 1 , 2 , 0 , 3 , 0 , 4 , 2 , 3 , 0 , 3 , 2 };
         
         int capacity = 4 ;
          
         System.out.println(pageFaults(pages, pages.length, capacity));
     }
}
// This code is contributed by Gaurav Miglani

C#

// C# implementation of above algorithm
using System;
using System.Collections.Generic;
  
class GFG
{
     // Method to find page faults 
     // using indexes
     static int pageFaults( int []pages, int n, int capacity)
     {
         // To represent set of current pages. 
         // We use an unordered_set so that 
         // we quickly check if a page is 
         // present in set or not
         HashSet< int > s = new HashSet< int >(capacity);
      
         // To store least recently used indexes
         // of pages.
         Dictionary< int , int > indexes = new Dictionary< int , int >();
      
         // Start from initial page
         int page_faults = 0;
         for ( int i = 0; i < n; i++)
         {
             // Check if the set can hold more pages
             if (s.Count < capacity)
             {
                 // Insert it into set if not present
                 // already which represents page fault
                 if (!s.Contains(pages[i]))
                 {
                     s.Add(pages[i]);
      
                     // increment page fault
                     page_faults++;
                 }
      
                 // Store the recently used index of
                 // each page
                 if (indexes.ContainsKey(pages[i]))
                     indexes[pages[i]] = i;
                 else
                     indexes.Add(pages[i], i);
             }
      
             // If the set is full then need to 
             // perform lru i.e. remove the least 
             // recently used page and insert
             // the current page
             else
             {
                 // Check if current page is not 
                 // already present in the set
                 if (!s.Contains(pages[i]))
                 {
                     // Find the least recently used pages
                     // that is present in the set
                     int lru = int .MaxValue, val = int .MinValue;
                                          
                     foreach ( int itr in s) 
                     {
                         int temp = itr;
                         if (indexes[temp] < lru)
                         {
                             lru = indexes[temp];
                             val = temp;
                         }
                     }
                  
                     // Remove the indexes page
                     s.Remove(val);
                      
                     //remove lru from hashmap
                     indexes.Remove(val);
                      
                     // insert the current page
                     s.Add(pages[i]);
      
                     // Increment page faults
                     page_faults++;
                 }
      
                 // Update the current page index
                 if (indexes.ContainsKey(pages[i]))
                     indexes[pages[i]] = i;
                 else
                     indexes.Add(pages[i], i);
             }
         }
         return page_faults;
     }
      
     // Driver Code
     public static void Main(String []args)
     {
         int []pages = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2};
          
         int capacity = 4;
          
         Console.WriteLine(pageFaults(pages, pages.Length, capacity));
     }
}
  
// This code is contributed by 29AjayKumar

输出如下：

6

另一种方法：

(不使用HashMap)

Java

// Java program for page replacement algorithms
import java.util.ArrayList;
  
public class LRU {
      
     // Driver method
     public static void main(String[] args) {
         int capacity = 4 ;
         int arr[] = { 7 , 0 , 1 , 2 , 0 , 3 , 0 , 4 , 2 , 3 , 0 , 3 , 2 };
          
         // To represent set of current pages.We use
         // an Arraylist
         ArrayList<Integer> s= new ArrayList<>(capacity);
         int count= 0 ;
         int page_faults= 0 ;
         for ( int i:arr)
         {
             // Insert it into set if not present
             // already which represents page fault
             if (!s.contains(i))
             {
              
             // Check if the set can hold equal pages
             if (s.size()==capacity)
             {
                 s.remove( 0 );
                 s.add(capacity- 1 , i);
             }
             else
                 s.add(count, i);
                 // Increment page faults
                 page_faults++;
                 ++count;
          
             }
             else
             {
                 // Remove the indexes page
                 s.remove((Object)i);
                 // insert the current page
                 s.add(s.size(), i);         
             }
          
         }
         System.out.println(page_faults);
     }
}

Python3

# Python3 program for page replacement algorithm
  
# Driver code
capacity = 4 
processList = [ 7 , 0 , 1 , 2 , 0 , 3 , 0 , 4 , 2 , 3 , 0 , 3 , 2 ]
                  
# List of current pages in Main Memory
s = [] 
  
pageFaults = 0
# pageHits = 0
  
for i in processList:
  
     # If i is not present in currentPages list
     if i not in s:
  
         # Check if the list can hold equal pages
         if ( len (s) = = capacity):
             s.remove(s[ 0 ])
             s.append(i)
  
         else :
             s.append(i)
  
         # Increment Page faults
         pageFaults + = 1
  
     # If page is already there in 
     # currentPages i.e in Main
     else :
          
         # Remove previous index of current page
         s.remove(i)
  
         # Now append it, at last index
         s.append(i)
      
print ( "{}" . format (pageFaults))
  
# This code is contributed by mahi_07

C#

// C# program for page replacement algorithms 
using System;
using System.Collections.Generic;
  
class LRU
{ 
      
     // Driver method 
     public static void Main(String[] args) 
     { 
         int capacity = 4; 
         int []arr = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2}; 
          
         // To represent set of current pages.
         // We use an Arraylist 
         List< int > s = new List< int >(capacity); 
         int count = 0; 
         int page_faults = 0; 
         foreach ( int i in arr) 
         { 
             // Insert it into set if not present 
             // already which represents page fault 
             if (!s.Contains(i)) 
             { 
              
             // Check if the set can hold equal pages 
             if (s.Count == capacity) 
             { 
                 s.RemoveAt(0); 
                 s.Insert(capacity - 1, i); 
             } 
             else
                 s.Insert(count, i); 
                  
                 // Increment page faults 
                 page_faults++; 
                 ++count; 
             } 
             else
             { 
                 // Remove the indexes page 
                 s.Remove(i); 
                  
                 // insert the current page 
                 s.Insert(s.Count, i);         
             } 
         } 
         Console.WriteLine(page_faults); 
     } 
} 
  
// This code is contributed by Rajput-Ji

输出如下：

6

注意：我们还可以找到页面点击数。只需维护一个单独的计数。

如果当前页面已在内存中, 则必须将其计为Page-hit。

我们将在其他集中讨论其他页面替换算法。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: