算法设计：如何计算三角形最短路径的最小长度？

本文概述

• 建议：在继续解决方案之前, 请先在{IDE}上尝试使用你的方法。
• C ++
• Java
• Python 3
• C#
• 的PHP

给定平面上的N个点，(X1, Y1) (X2, Y2) (X3, Y3) ...... (XN, YN)任务是计算三角形短边的最小长度。以及在坐标轴(X轴和Y轴)上放置等腰三角形任意两条边的路径或点，以覆盖所有点。

注意：如果点位于三角形内部或三角形侧面, 则将覆盖该点。

例子：

Input: (1, 3), (1, 1), (2, 1), (2, 2) Output: Length -> 4 , Path -> ( 1, 4 ) and ( 4, 1 ) Input: (1, 2), (1, 1), (2, 1) Output: Length -> 3 , Path -> ( 1, 3 ) and ( 3, 1 )

推荐：请尝试以下方法{IDE}首先, 在继续解决方案之前。

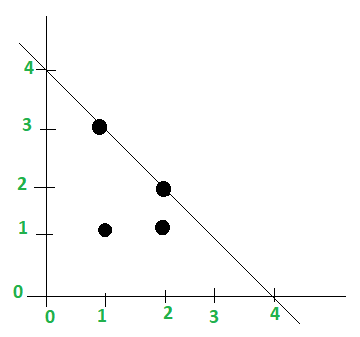
在第一个示例中, 最短路径的最小长度等于点的最大和, 即1 + 3或2 + 2。因此, 将覆盖所有点的路径在坐标轴上为(1, 4)和(4, 1)。

以下是解决此问题的分步算法：

1. 在平面上初始化" N"个点。
2. 遍历每个点, 找到每个点的总和, 并将其存储在变量"答案"中。
3. 用下一个总和替换下一个最大的总和。
4. 然后, 你将获得坐标轴(1, answer)和(answer, 1)上的路径, 该路径将覆盖等腰三角形的所有点。

下面是上述算法的实现：

C ++

// C++ program to illustrate
// the above problem
#include <bits/stdc++.h>
using namespace std;
#define ll long long
  
// function to get the minimum length of
// the shorter side of the triangle
void shortestLength( int n, int x[], int y[])
{
         int answer = 0;
  
     // traversing through each points on the plane
     int i = 0;
     while (n--) {
         // if sum of a points is greater than the
         // previous one, the maximum gets replaced
         if (x[i] + y[i] > answer)
             answer = x[i] + y[i];
  
         i++;
     }
  
     // print the length
     cout << "Length -> " << answer << endl;
     cout << "Path -> "
          << "( 1, " << answer << " )"
          << "and ( " << answer << ", 1 )" ;
}
  
// Driver code
int main()
{
     // initialize the number of points
     int n = 4;
  
     // points on the plane
     int x[n] = { 1, 4, 2, 1 };
     int y[n] = { 4, 1, 1, 2 };
  
     shortestLength(n, x, y);
  
     return 0;
}

Java

// Java program to illustrate 
// the above problem 
class GFG
{
  
// function to get the minimum length of 
// the shorter side of the triangle 
static void shortestLength( int n, int x[], int y[]) 
{ 
     int answer = 0 ; 
  
     // traversing through each 
     // points on the plane 
     int i = 0 ; 
     while (n != 0 && i < x.length)
     { 
         // if sum of a points is greater
         // than the previous one, the 
         // maximum gets replaced 
         if (x[i] + y[i] > answer) 
             answer = x[i] + y[i]; 
  
         i++; 
     } 
  
     // print the length 
     System.out.println( "Length -> " + answer ); 
     System.out.println( "Path -> " + 
                        "( 1, " + answer + " )" + 
                        "and ( " + answer + ", 1 )" ); 
} 
  
// Driver code 
public static void main(String[] args) 
{ 
     // initialize the number of points 
     int n = 4 ; 
  
     // points on the plane 
     int x[] = new int [] { 1 , 4 , 2 , 1 }; 
     int y[] = new int [] { 4 , 1 , 1 , 2 }; 
  
     shortestLength(n, x, y); 
} 
}
  
// This code is contributed 
// by Prerna Saini

Python 3

# Python 3 program to illustrate
# the above problem
  
# function to get the minimum length of
# the shorter side of the triangle
def shortestLength(n, x, y):
     answer = 0
  
     # traversing through each
     # points on the plane
     i = 0
     while n > 0 : 
          
         # if sum of a points is greater 
         # than the previous one, the 
         # maximum gets replaced
         if (x[i] + y[i] > answer):
             answer = x[i] + y[i]
  
         i + = 1
         n - = 1
  
     # print the length
     print ( "Length -> " + str (answer))
     print ( "Path -> " +
         "( 1, " + str (answer) + " )" +
         "and ( " + str ( answer) + ", 1 )" )
  
# Driver code
if __name__ = = "__main__" :
      
     # initialize the number of points
     n = 4
  
     # points on the plane
     x = [ 1 , 4 , 2 , 1 ]
     y = [ 4 , 1 , 1 , 2 ] 
     shortestLength(n, x, y)
  
# This code is contributed 
# by ChitraNayal

C#

// C# program to illustrate 
// the above problem 
using System;
  
class GFG
{
  
// function to get the minimum 
// length of the shorter side 
// of the triangle 
static void shortestLength( int n, int [] x, int [] y) 
{ 
     int answer = 0; 
  
     // traversing through each 
     // points on the plane 
     int i = 0; 
     while (n != 0 && i < x.Length)
     { 
         // if sum of a points is greater
         // than the previous one, the 
         // maximum gets replaced 
         if (x[i] + y[i] > answer) 
             answer = x[i] + y[i]; 
  
         i++; 
     } 
  
     // print the length 
     Console.WriteLine( "Length -> " + answer); 
     Console.WriteLine( "Path -> " + 
                       "( 1, " + answer + " )" + 
                       "and ( " + answer + ", 1 )" ); 
} 
  
// Driver code
static public void Main ()
{
      
     // initialize the 
     // number of points 
     int n = 4; 
  
     // points on the plane 
     int [] x = new int [] { 1, 4, 2, 1 }; 
     int [] y = new int [] { 4, 1, 1, 2 }; 
  
     shortestLength(n, x, y); 
}
}
  
// This code is contributed by Mahadev

的PHP

<?php 
// PHP program to illustrate
// the above problem
  
// function to get the minimum length of
// the shorter side of the triangle
function shortestLength( $n , & $x , & $y )
{
     $answer = 0;
  
     // traversing through each 
     // points on the plane
     $i = 0;
     while ( $n --)
     {
          
         // if sum of a points is greater 
         // than the previous one, the 
         // maximum gets replaced
         if ( $x [ $i ] + $y [ $i ] > $answer )
             $answer = $x [ $i ] + $y [ $i ];
  
         $i ++;
     }
  
     // print the length
     echo "Length -> " . $answer . "\n" ;
     echo "Path -> " . "( 1, " . $answer . " )" .
          "and ( " . $answer . ", 1 )" ;
}
  
// Driver code
  
// initialize the number of points
$n = 4;
  
// points on the plane
$x = array (1, 4, 2, 1 );
$y = array (4, 1, 1, 2 );
  
shortestLength( $n , $x , $y );
  
// This code is contributed 
// by ChitraNayal
?>

输出如下：

Length -> 5
Path -> ( 1, 5 )and ( 5, 1 )

---