算法：在二叉搜索树中找到最小值的节点

2021年3月17日18:01:29 发表评论 791 次浏览

本文概述

这很简单。只需递归地从根到节点遍历该节点, 直到left为NULL。左侧为NULL的节点是最小值的节点。

BST_LCA

推荐：请在"实践首先, 在继续解决方案之前。

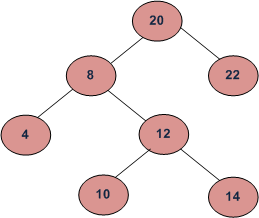
对于上面的树, 我们从20开始, 然后向左移动8, 继续向左移动, 直到看到NULL。由于4的左边为NULL, 因此4是具有最小值的节点。

C ++

//C++ program to find minimum value node in binary search Tree. 
#include <bits/stdc++.h> 
using namespace std; 
  
/* A binary tree node has data, pointer to left child 
and a pointer to right child */
struct node 
{ 
     int data; 
     struct node* left; 
     struct node* right; 
}; 
  
/* Helper function that allocates a new node 
with the given data and NULL left and right 
pointers. */
struct node* newNode( int data) 
{ 
struct node* node = ( struct node*) 
                     malloc ( sizeof ( struct node)); 
node->data = data; 
node->left = NULL; 
node->right = NULL; 
  
return (node); 
} 
  
/* Give a binary search tree and a number, inserts a new node with the given number in 
the correct place in the tree. Returns the new 
root pointer which the caller should then use 
(the standard trick to avoid using reference 
parameters). */
struct node* insert( struct node* node, int data) 
{ 
/* 1. If the tree is empty, return a new, single node */
if (node == NULL) 
     return (newNode(data)); 
else
{ 
     /* 2. Otherwise, recur down the tree */
     if (data <= node->data) 
         node->left = insert(node->left, data); 
     else
         node->right = insert(node->right, data); 
  
     /* return the (unchanged) node pointer */
     return node; 
} 
} 
  
/* Given a non-empty binary search tree, return the minimum data value found in that 
tree. Note that the entire tree does not need 
to be searched. */
int minValue( struct node* node) 
{ 
struct node* current = node; 
  
/* loop down to find the leftmost leaf */
while (current->left != NULL) 
{ 
     current = current->left; 
} 
return (current->data); 
} 
  
/* Driver Code*/
int main() 
{ 
struct node* root = NULL; 
root = insert(root, 4); 
insert(root, 2); 
insert(root, 1); 
insert(root, 3); 
insert(root, 6); 
insert(root, 5); 
  
cout << "\n Minimum value in BST is " << minValue(root); 
getchar (); 
return 0; 
} 
  
// This code is contributed by Mukul Singh.

C

#include <stdio.h>
#include<stdlib.h>
  
/* A binary tree node has data, pointer to left child 
    and a pointer to right child */
struct node 
{
     int data;
     struct node* left;
     struct node* right;
};
  
/* Helper function that allocates a new node 
with the given data and NULL left and right 
pointers. */
struct node* newNode( int data) 
{
   struct node* node = ( struct node*)
                        malloc ( sizeof ( struct node));
   node->data  = data;
   node->left  = NULL;
   node->right = NULL;
    
   return (node);
}
  
/* Give a binary search tree and a number, inserts a new node with the given number in 
the correct place in the tree. Returns the new 
root pointer which the caller should then use 
(the standard trick to avoid using reference 
parameters). */
struct node* insert( struct node* node, int data) 
{
   /* 1. If the tree is empty, return a new, single node */
   if (node == NULL) 
     return (newNode(data));  
   else 
   {
     /* 2. Otherwise, recur down the tree */
     if (data <= node->data) 
         node->left  = insert(node->left, data);
     else 
         node->right = insert(node->right, data);
    
     /* return the (unchanged) node pointer */
     return node; 
   }
}
  
/* Given a non-empty binary search tree, return the minimum data value found in that 
tree. Note that the entire tree does not need 
to be searched. */
int minValue( struct node* node) {
   struct node* current = node;
  
   /* loop down to find the leftmost leaf */
   while (current->left != NULL) {
     current = current->left;
   }
   return (current->data);
}
  
/* Driver program to test sameTree function*/    
int main()
{
   struct node* root = NULL;
   root = insert(root, 4);
   insert(root, 2);
   insert(root, 1);
   insert(root, 3);
   insert(root, 6);
   insert(root, 5);  
  
   printf ( "\n Minimum value in BST is %d" , minValue(root));
   getchar ();
   return 0;    
}

Java

// Java program to find minimum value node in Binary Search Tree
  
// A binary tree node
class Node {
  
     int data;
     Node left, right;
  
     Node( int d) {
         data = d;
         left = right = null ;
     }
}
  
class BinaryTree {
  
     static Node head;
      
     /* Given a binary search tree and a number, inserts a new node with the given number in 
      the correct place in the tree. Returns the new 
      root pointer which the caller should then use 
      (the standard trick to avoid using reference 
      parameters). */
     Node insert(Node node, int data) {
          
         /* 1. If the tree is empty, return a new, single node */
         if (node == null ) {
             return ( new Node(data));
         } else {
              
             /* 2. Otherwise, recur down the tree */
             if (data <= node.data) {
                 node.left = insert(node.left, data);
             } else {
                 node.right = insert(node.right, data);
             }
  
             /* return the (unchanged) node pointer */
             return node;
         }
     }
  
     /* Given a non-empty binary search tree, return the minimum data value found in that 
      tree. Note that the entire tree does not need 
      to be searched. */
     int minvalue(Node node) {
         Node current = node;
  
         /* loop down to find the leftmost leaf */
         while (current.left != null ) {
             current = current.left;
         }
         return (current.data);
     }
      
     // Driver program to test above functions
     public static void main(String[] args) {
         BinaryTree tree = new BinaryTree();
         Node root = null ;
         root = tree.insert(root, 4 );
         tree.insert(root, 2 );
         tree.insert(root, 1 );
         tree.insert(root, 3 );
         tree.insert(root, 6 );
         tree.insert(root, 5 );
  
         System.out.println( "Minimum value of BST is " + tree.minvalue(root));
     }
}
  
// This code is contributed by Mayank Jaiswal

python

# Python program to find the node with minimum value in bst
  
# A binary tree node
class Node:
  
     # Constructor to create a new node
     def __init__( self , key):
         self .data = key
         self .left = None
         self .right = None
  
""" Give a binary search tree and a number, inserts a new node with the given number in 
the correct place in the tree. Returns the new 
root pointer which the caller should then use 
(the standard trick to avoid using reference 
parameters). """
def insert(node, data):
  
     # 1. If the tree is empty, return a new, # single node
     if node is None :
         return (Node(data))
  
     else :
         # 2. Otherwise, recur down the tree
         if data < = node.data:
             node.left = insert(node.left, data)
         else :
             node.right = insert(node.right, data)
  
         # Return the (unchanged) node pointer
         return node
  
""" Given a non-empty binary search tree, return the minimum data value found in that 
tree. Note that the entire tree does not need 
to be searched. """
def minValue(node):
     current = node
  
     # loop down to find the lefmost leaf
     while (current.left is not None ):
         current = current.left
  
     return current.data
  
# Driver program
root = None
root = insert(root, 4 )
insert(root, 2 )
insert(root, 1 )
insert(root, 3 )
insert(root, 6 )
insert(root, 5 )
  
print "\nMinimum value in BST is %d"  % (minValue(root))
  
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

using System;
  
// C# program to find minimum value node in Binary Search Tree 
  
// A binary tree node 
public class Node
{
  
     public int data;
     public Node left, right;
  
     public Node( int d)
     {
         data = d;
         left = right = null ;
     }
}
  
public class BinaryTree
{
  
     public static Node head;
  
     /* Given a binary search tree and a number, inserts a new node with the given number in  
      the correct place in the tree. Returns the new  
      root pointer which the caller should then use  
      (the standard trick to avoid using reference  
      parameters). */
     public virtual Node insert(Node node, int data)
     {
  
         /* 1. If the tree is empty, return a new, single node */
         if (node == null )
         {
             return ( new Node(data));
         }
         else
         {
  
             /* 2. Otherwise, recur down the tree */
             if (data <= node.data)
             {
                 node.left = insert(node.left, data);
             }
             else
             {
                 node.right = insert(node.right, data);
             }
  
             /* return the (unchanged) node pointer */
             return node;
         }
     }
  
     /* Given a non-empty binary search tree, return the minimum data value found in that  
      tree. Note that the entire tree does not need  
      to be searched. */
     public virtual int minvalue(Node node)
     {
         Node current = node;
  
         /* loop down to find the leftmost leaf */
         while (current.left != null )
         {
             current = current.left;
         }
         return (current.data);
     }
  
     // Driver program to test above functions 
     public static void Main( string [] args)
     {
         BinaryTree tree = new BinaryTree();
         Node root = null ;
         root = tree.insert(root, 4);
         tree.insert(root, 2);
         tree.insert(root, 1);
         tree.insert(root, 3);
         tree.insert(root, 6);
         tree.insert(root, 5);
  
         Console.WriteLine( "Minimum value of BST is " + tree.minvalue(root));
     }
}
  
   // This code is contributed by Shrikant13

的PHP

<?php
// PHP program to find the node with 
// minimum value in bst
  
// create a binary tree
class node 
{
     private $node , $left , $right ;
     function __construct( $node ) 
     {
         $this ->node = $node ;
         $left = $right = NULL;
     }
  
     // set the left node in tree
     function set_left( $left ) 
     {
         $this ->left = $left ;
     }
  
     // set the right node in tree
     function set_right( $right ) 
     {
         $this ->right = $right ;
     }
  
     // get left node 
     function get_left()
     {
         return $this ->left;
     }
  
     // get right node 
     function get_right()
     {
         return $this ->right;
     }
  
     // get value of current node
     function get_node()
     {
         return $this ->node;
     }
      
}
  
// Find the node with minimum value 
// in a Binary Search Tree
function get_minimum_value( $node ) 
{
     /*travel till last left node to 
       get the minimum value*/
     while ( $node ->get_left() != NULL) 
     {
         $node = $node ->get_left();
     }
     return $node ->get_node();
}
  
// code to creating a tree 
$node = new node(4);
$lnode = new node(2); 
$lnode ->set_left( new node(1));
$lnode ->set_right( new node(3));
$rnode = new node(6);
$rnode ->set_left( new node(5));
$node ->set_left( $lnode );
$node ->set_right( $rnode );
  
$minimum_value = get_minimum_value( $node );
echo 'Minimum value of BST is ' . 
                  $minimum_value ;
  
// This code is contributed
// by Deepika Pathak
?>

输出如下：

Minimum value in BST is 1

时间复杂度：

O(n)最坏的情况发生在左偏斜的树上。

类似地, 我们可以通过递归遍历二叉搜索树的右节点来获得最大值。

参考文献：

http://cslibrary.stanford.edu/110/BinaryTrees.html

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: