计算最大流：Push Relabel算法|S2（算法代码实现）

2021年3月15日09:51:46 发表评论 1,260 次浏览

我们强烈建议在继续本文之前先参考以下文章。

Push-Relabel算法|S1(简介和插图)

问题陈述：给定一个表示流网络的图形, 其中每个边都有容量。也给出了两个顶点资源" s"和水槽在图表中的" t"处, 找到具有以下约束的从s到t的最大可能流量：

a)边缘的流量不超过边缘的给定容量。

b)除s和t以外, 每个顶点的流入流量等于流出流量。

例如, 请考虑以下CLRS书中的图表。

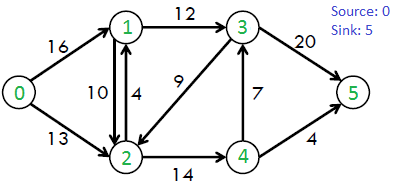
上图中的最大可能流量为23。

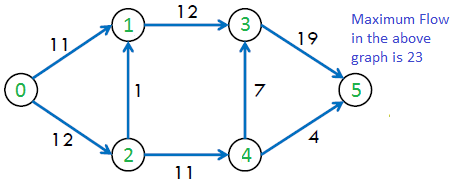
Push-Relabel Algorithm 
1) Initialize PreFlow : Initialize Flows and Heights 

2) While it is possible to perform a Push() or Relablel() on a vertex
   // Or while there is a vertex that has excess flow
           Do Push() or Relabel()

// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.

以下是Push Relabel 算法中执行的主要操作。

Push-Relabel算法中有三个主要操作

初始化PreFlow()它初始化所有顶点的高度和流。

Preflow() 
1) Initialize height and flow of every vertex as 0.
2) Initialize height of source vertex equal to total 
   number of vertices in graph.
3) Initialize flow of every edge as 0.
4) For all vertices adjacent to source s, flow and  
   excess flow is equal to capacity initially.

push()用于从流量过大的节点产生流量。如果顶点有多余的流动, 并且有一个相邻的高度较小(在残差图中), 我们将流动从顶点推到相邻的较低高度。通过管道(边缘)的推动流量等于多余流量和边缘容量的最小值。
Relabel()当顶点有多余的流量且相邻的顶点都不处于较低高度时, 将使用操作。我们基本上增加了顶点的高度, 以便可以执行push()。为了增加高度, 我们选择相邻的最小高度(在残差图中, 即可以添加流量的相邻高度)并对其加1。

实现

以下实现使用以下结构来表示流网络。

struct Vertex 
{
   int h;      // Height of node
   int e_flow; // Excess Flow 
}

struct Edge 
{
   int u, v; // Edge is from u to v       
   int flow; // Current flow
   int capacity; 
}

class Graph 
{
   Edge edge[];   // Array of edges
   Vertex ver[];  // Array of vertices 
}

以下代码将给定的图形本身用作流网络和残差图。我们没有为残差图创建单独的图, 并且为简单起见使用了相同的图。

// C++ program to implement push-relabel algorithm for
// getting maximum flow of graph
#include <bits/stdc++.h>
using namespace std;
  
struct Edge
{
     // To store current flow and capacity of edge
     int flow, capacity;
  
     // An edge u--->v has start vertex as u and end
     // vertex as v.
     int u, v;
  
     Edge( int flow, int capacity, int u, int v)
     {
         this ->flow = flow;
         this ->capacity = capacity;
         this ->u = u;
         this ->v = v;
     }
};
  
// Represent a Vertex
struct Vertex
{
     int h, e_flow;
  
     Vertex( int h, int e_flow)
     {
         this ->h = h;
         this ->e_flow = e_flow;
     }
};
  
// To represent a flow network
class Graph
{
     int V;    // No. of vertices
     vector<Vertex> ver;
     vector<Edge> edge;
  
     // Function to push excess flow from u
     bool push( int u);
  
     // Function to relabel a vertex u
     void relabel( int u);
  
     // This function is called to initialize
     // preflow
     void preflow( int s);
  
     // Function to reverse edge
     void updateReverseEdgeFlow( int i, int flow);
  
public :
     Graph( int V);  // Constructor
  
     // function to add an edge to graph
     void addEdge( int u, int v, int w);
  
     // returns maximum flow from s to t
     int getMaxFlow( int s, int t);
};
  
Graph::Graph( int V)
{
     this ->V = V;
  
     // all vertices are initialized with 0 height
     // and 0 excess flow
     for ( int i = 0; i < V; i++)
         ver.push_back(Vertex(0, 0));
}
  
void Graph::addEdge( int u, int v, int capacity)
{
     // flow is initialized with 0 for all edge
     edge.push_back(Edge(0, capacity, u, v));
}
  
void Graph::preflow( int s)
{
     // Making h of source Vertex equal to no. of vertices
     // Height of other vertices is 0.
     ver展开.h = ver.size();
  
     //
     for ( int i = 0; i < edge.size(); i++)
     {
         // If current edge goes from source
         if (edge[i].u == s)
         {
             // Flow is equal to capacity
             edge[i].flow = edge[i].capacity;
  
             // Initialize excess flow for adjacent v
             ver[edge[i].v].e_flow += edge[i].flow;
  
             // Add an edge from v to s in residual graph with
             // capacity equal to 0
             edge.push_back(Edge(-edge[i].flow, 0, edge[i].v, s));
         }
     }
}
  
// returns index of overflowing Vertex
int overFlowVertex(vector<Vertex>& ver)
{
     for ( int i = 1; i < ver.size() - 1; i++)
        if (ver[i].e_flow > 0)
             return i;
  
     // -1 if no overflowing Vertex
     return -1;
}
  
// Update reverse flow for flow added on ith Edge
void Graph::updateReverseEdgeFlow( int i, int flow)
{
     int u = edge[i].v, v = edge[i].u;
  
     for ( int j = 0; j < edge.size(); j++)
     {
         if (edge[j].v == v && edge[j].u == u)
         {
             edge[j].flow -= flow;
             return ;
         }
     }
  
     // adding reverse Edge in residual graph
     Edge e = Edge(0, flow, u, v);
     edge.push_back(e);
}
  
// To push flow from overflowing vertex u
bool Graph::push( int u)
{
     // Traverse through all edges to find an adjacent (of u)
     // to which flow can be pushed
     for ( int i = 0; i < edge.size(); i++)
     {
         // Checks u of current edge is same as given
         // overflowing vertex
         if (edge[i].u == u)
         {
             // if flow is equal to capacity then no push
             // is possible
             if (edge[i].flow == edge[i].capacity)
                 continue ;
  
             // Push is only possible if height of adjacent
             // is smaller than height of overflowing vertex
             if (ver[u].h > ver[edge[i].v].h)
             {
                 // Flow to be pushed is equal to minimum of
                 // remaining flow on edge and excess flow.
                 int flow = min(edge[i].capacity - edge[i].flow, ver[u].e_flow);
  
                 // Reduce excess flow for overflowing vertex
                 ver[u].e_flow -= flow;
  
                 // Increase excess flow for adjacent
                 ver[edge[i].v].e_flow += flow;
  
                 // Add residual flow (With capacity 0 and negative
                 // flow)
                 edge[i].flow += flow;
  
                 updateReverseEdgeFlow(i, flow);
  
                 return true ;
             }
         }
     }
     return false ;
}
  
// function to relabel vertex u
void Graph::relabel( int u)
{
     // Initialize minimum height of an adjacent
     int mh = INT_MAX;
  
     // Find the adjacent with minimum height
     for ( int i = 0; i < edge.size(); i++)
     {
         if (edge[i].u == u)
         {
             // if flow is equal to capacity then no
             // relabeling
             if (edge[i].flow == edge[i].capacity)
                 continue ;
  
             // Update minimum height
             if (ver[edge[i].v].h < mh)
             {
                 mh = ver[edge[i].v].h;
  
                 // updating height of u
                 ver[u].h = mh + 1;
             }
         }
     }
}
  
// main function for printing maximum flow of graph
int Graph::getMaxFlow( int s, int t)
{
     preflow(s);
  
     // loop untill none of the Vertex is in overflow
     while (overFlowVertex(ver) != -1)
     {
         int u = overFlowVertex(ver);
         if (!push(u))
             relabel(u);
     }
  
     // ver.back() returns last Vertex, whose
     // e_flow will be final maximum flow
     return ver.back().e_flow;
}
  
// Driver program to test above functions
int main()
{
     int V = 6;
     Graph g(V);
  
     // Creating above shown flow network
     g.addEdge(0, 1, 16);
     g.addEdge(0, 2, 13);
     g.addEdge(1, 2, 10);
     g.addEdge(2, 1, 4);
     g.addEdge(1, 3, 12);
     g.addEdge(2, 4, 14);
     g.addEdge(3, 2, 9);
     g.addEdge(3, 5, 20);
     g.addEdge(4, 3, 7);
     g.addEdge(4, 5, 4);
  
     // Initialize source and sink
     int s = 0, t = 5;
  
     cout << "Maximum flow is " << g.getMaxFlow(s, t);
     return 0;
}

输出如下