给定一个表示流网络的图形, 其中每个边都有容量。也给出了两个顶点资源" s"和水槽在图表中的" t"处, 找到具有以下约束的从s到t的最大可能流量:
a)边缘的流量不超过边缘的给定容量。
b)除s和t以外, 每个顶点的流入流量等于流出流量。
例如, 请考虑以下CLRS书中的图表。
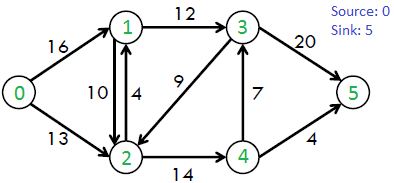
上图中的最大可能流量为23。
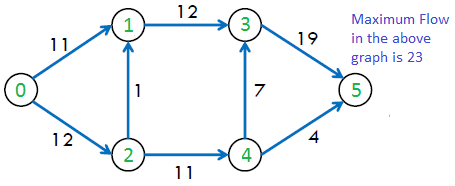
我们已经讨论过Ford-Fulkerson算法使用扩充路径来计算最大流量。
Push-Relabel方法比Ford-Fulkerson算法更有效。在这篇文章中, 讨论了Goldberg的"通用"最大流量算法, 该算法在(2E)时间。此时间复杂度优于O(E2V), 这是Edmond-Karp算法(基于BFS的Ford-Fulkerson实现)的时间复杂度。存在一种基于推-重新标记方法的算法, 可在O(V3)甚至比这里讨论的更好。
与Ford-Fulkerson的相似之处
- 与Ford-Fulkerson一样, Push-Relabel也适用于残差图(流网络的残差图是指示其他可能流量的图。如果残差图中存在从源到汇的路径, 则可以添加流量) 。
与Ford-Fulkerson的差异
- Push-Relabel算法在更局限的地方工作。Push-Relabel算法一次不会在一个顶点上工作, 而不是检查整个残差网络以找到增广路径(来源:CLRS书)。
- 在Ford-Fulkerson中, 每个顶点(源和汇除外)的总流出和总流入之间的净差保持为0。Push-Relabel算法允许流入超过最终流出之前的流出。在最终流中, 除源和接收器外, 所有其他器的净差为0。
- 时间复杂度明智地提高了效率。
Push-Relabel算法(考虑流体流动问题)背后的直觉是, 我们将边视为水管和节点是关节。该水源被认为是最高水位, 它将水输送到所有相邻节点。一旦节点有多余的水, 推将水浇到较小的高度节点。如果水被局部困在某个顶点, 则该顶点为重新贴上标签这意味着它的高度增加了。
以下是在进行算法之前要考虑的一些有用事实。
- 每个顶点都有一个高度变量和一个多余流量。高度用于确定顶点是否可以将流推向相邻顶点(顶点只能将流推向较小的高度顶点)。流量过大是流入顶点的总流量减去流出顶点的总流量之差。
Excess Flow of u = Total Inflow to u - Total Outflow from u - 像Ford-Fulkerson。每个边都与之相关流(表示当前流量)和一个容量
以下是完整算法的抽象步骤。
Push-Relabel Algorithm
1) Initialize PreFlow : Initialize Flows
and Heights
2) While it is possible to perform a Push() or
Relablel() on a vertex
// Or while there is a vertex that has excess flow
Do Push() or Relabel()
// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.Push-Relabel算法中有三个主要操作
- 初始化PreFlow()它初始化所有顶点的高度和流。
Preflow() 1) Initialize height and flow of every vertex as 0. 2) Initialize height of source vertex equal to total number of vertices in graph. 3) Initialize flow of every edge as 0. 4) For all vertices adjacent to source s, flow and excess flow is equal to capacity initially.
- 推()用于从流量过大的节点产生流量。如果顶点有多余的流动, 并且有一个相邻的高度较小(在残差图中), 我们将流动从顶点推到相邻的较低高度。通过管道(边缘)的推动流量等于多余流量和边缘容量的最小值。
- Relabel()当顶点有多余的流量且相邻的顶点都不处于较低高度时, 将使用操作。我们基本上增加了顶点的高度, 以便可以执行push()。为了增加高度, 我们选择相邻的最小高度(在残差图中, 即可以添加流量的相邻高度)并对其加1。
请注意, 以上操作是在残差图上执行的(例如福特福克森)。
插图:
在继续下面的示例之前, 我们需要确保我们了解残差图(请参见
这个
有关残差图的更多详细信息)。残差图与所示的图不同。
每当我们将顶点u的流推入或添加到v时, 我们都会在残差图中进行以下更新:
1)我们从u到v的边缘容量中减去流量。如果边缘的容量变为0, 则该边缘不再存在于残差图中。
2)我们将流量增加到从v到u的边容量。
For example, consider two vertices u an v.
In original graph
3/10
u ---------> v
3 is current flow from u to v and
10 is capacity of edge from u to v.
In residual Graph, there are two edges corresponding
to one edge shown above.
7
u ---------> v
3
u <--------- v初始给定流程图。
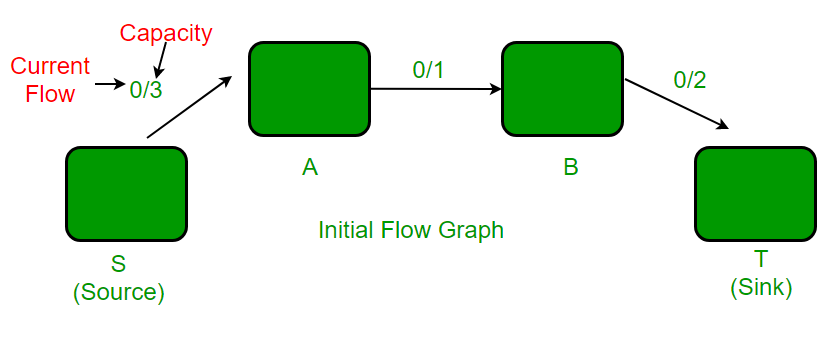
.
在PreFlow操作之后。在残差图中, 从A到S的边为容量3, 从S到A没有边。
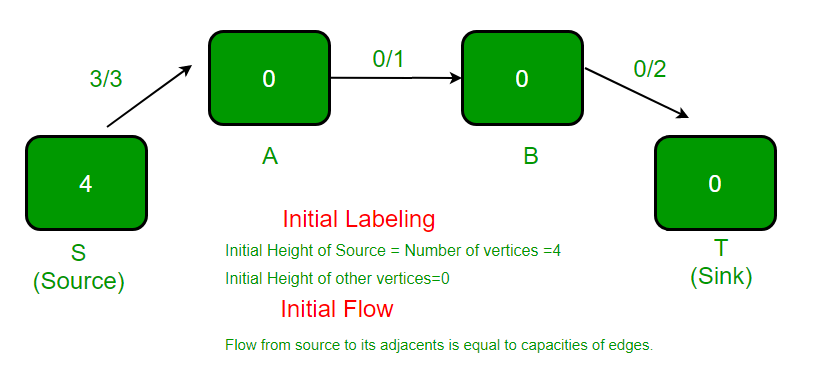
.
高亮显示的顶点被重新标记(高度变为1), 因为它有过多的流量, 并且没有相邻的顶点具有较小的高度。新高度等于相邻高度的最小值加1。在残差图中, 顶点A有两个相邻, 一个是S, 另一个是B。S的高度是4, B的高度是0。这两个的最小值heights是0。我们取最小值并加1。
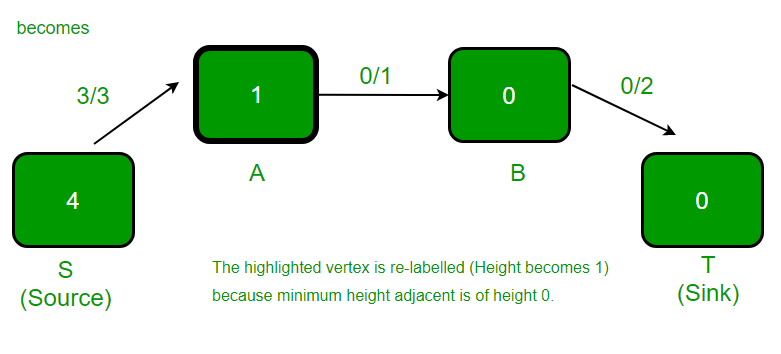
.
突出显示的顶点有过多的流动, 并且相邻的顶点的高度较低, 因此发生push()。顶点A的多余流量为2, 边(A, B)的容量为1。因此, 推动的流量为1(两个值的最小值)。
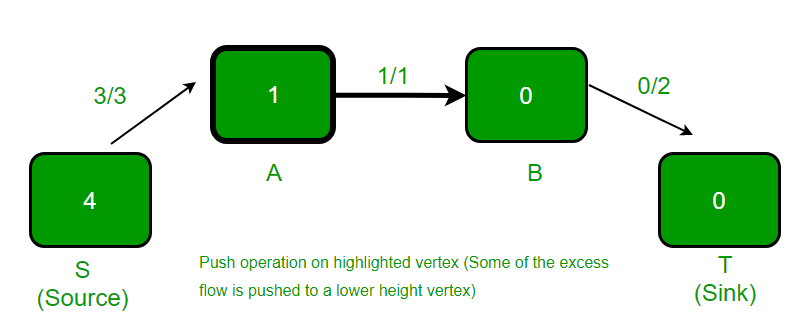
.
高亮显示的顶点被重新标记(高度变为1), 因为它有过多的流量, 并且没有相邻的顶点具有较小的高度。
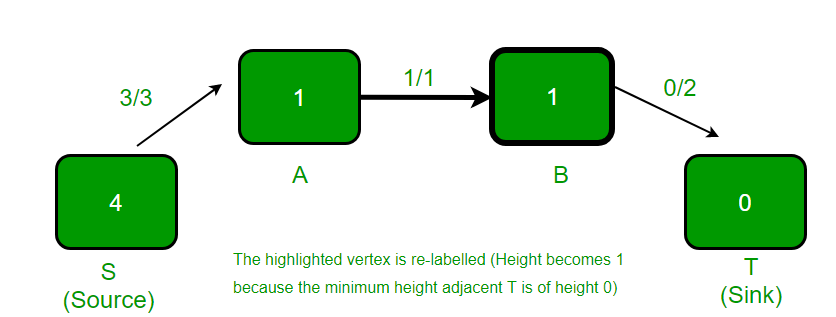
.
突出显示的顶点有多余的流量, 并且相邻的顶点的高度较低, 因此flow()从B推到T。
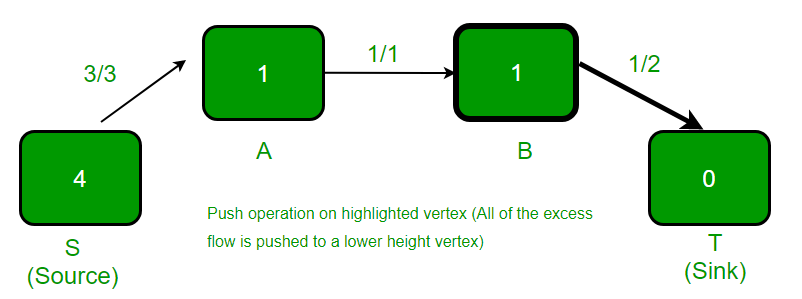
.
高亮显示的顶点被重新标记(高度变为5), 因为它有过多的流量, 并且没有相邻的顶点具有较小的高度。
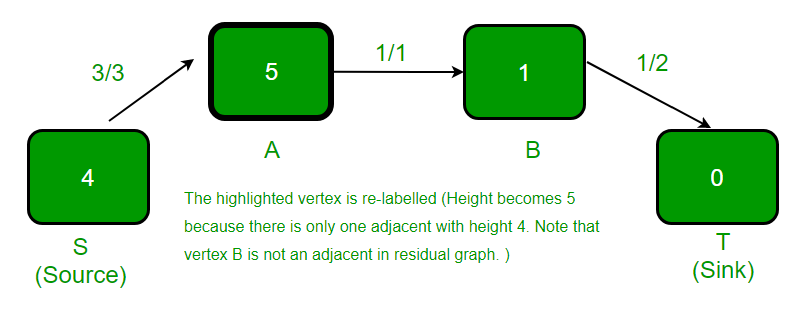
.
突出显示的顶点有过多的流动, 并且相邻的顶点的高度较低, 因此发生push()。
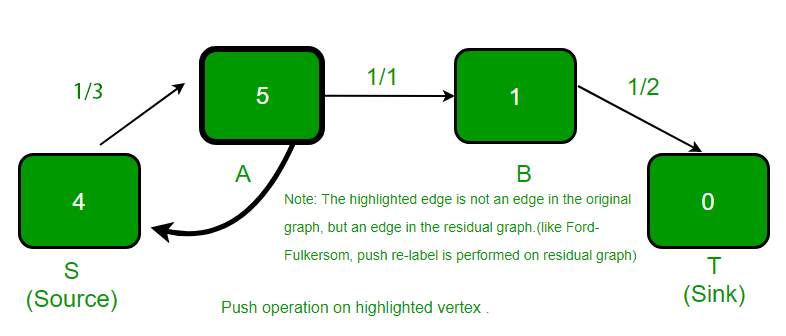
.
高亮显示的顶点被重新标记(高度增加1), 因为它有过多的流量, 并且没有相邻的顶点具有较小的高度。
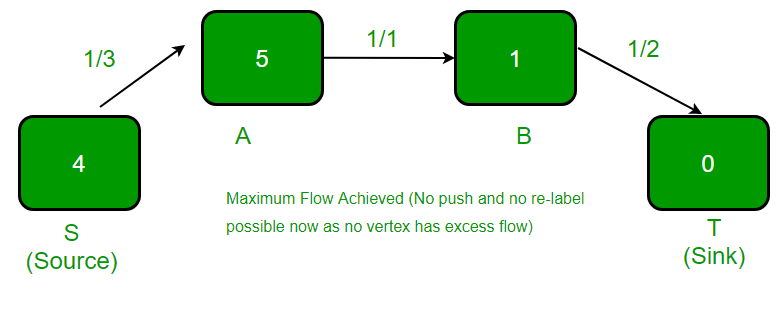
上面的例子取自这里.
推重贴标签算法|套装2(实施)
本文作者:悉达思·拉尔瓦尼(Siddharth Lalwani)。如果你喜欢lsbin并希望做出贡献, 那么你也可以写一篇文章并将你的文章邮寄到contribution@lsbin.org。查看你的文章出现在lsbin主页上, 并帮助其他Geeks。
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)