0-1 BFS（二值权图中的最短路径）介绍和代码实现

2021年3月14日14:44:15 发表评论 1,493 次浏览

本文概述

建议：在继续解决方案之前, 请先在{IDE}上尝试使用你的方法。
C ++
Java
Python3

给定一个图, 其中每个边的权重为0或1。在图中还给出了源顶点。查找从源顶点到其他每个顶点的最短路径。

例子：

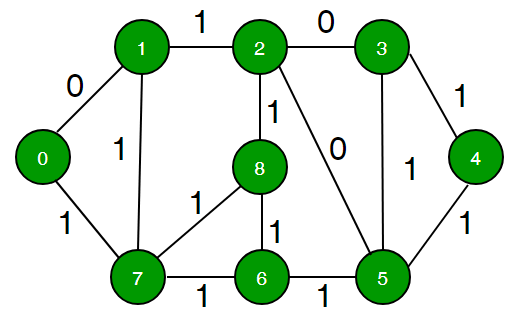
Input : Source Vertex = 0 and below graph 


Output : Shortest distances from given source
         0 0 1 1 2 1 2 1 2

Explanation : 
Shortest distance from 0 to 0 is 0
Shortest distance from 0 to 1 is 0
Shortest distance from 0 to 2 is 1
..................

推荐：请尝试以下方法{IDE}首先, 在继续解决方案之前。

在正常情况下BFS图中所有边缘的权重相等, 但在0-1 BFS中, 某些边缘的权重为0, 而某些边缘的权重为1。在这种情况下, 我们将不使用布尔数组来标记访问的节点, 但是在每一步中, 我们都会检查最佳距离条件。我们用双头队列存储节点。在执行BFS时, 如果找到权重= 0的边, 则将节点推入双头队列的前面, 如果找到权重= 1的边, 则将其推入双头队列的后面。

该方法类似于迪克斯特拉如果前一节点放宽了到节点的最短距离, 则只有将其推入队列。

以上想法适用于所有情况, 当弹出一个顶点(如Dijkstra)时, 它是剩余顶点中最小的权重顶点。如果相邻的权重顶点为0, 则该相邻顶点的距离相同。如果相邻的权重为1, 则该相邻的对象在出队的所有顶点之间具有最大距离(因为所有其他顶点都与当前弹出的顶点相邻或与先前弹出的顶点相邻)。

以下是上述想法的实现。

C ++

// C++ program to implement single source
// shortest path for a Binary Graph
#include<bits/stdc++.h>
using namespace std;
  
/* no.of vertices */
#define V 9
  
// a structure to represent edges
struct node
{
     // two variable one denote the node
     // and other the weight
     int to, weight;
};
  
// vector to store edges
vector <node> edges[V];
  
// Prints shortest distance from given source to
// every other vertex
void zeroOneBFS( int src)
{
     // Initialize distances from given source
     int dist[V];
     for ( int i=0; i<V; i++)
         dist[i] = INT_MAX;
  
     // double ende queue to do BFS.
     deque < int > Q;
     dist[src] = 0;
     Q.push_back(src);
  
     while (!Q.empty())
     {
         int v = Q.front();
         Q.pop_front();
  
         for ( int i=0; i<edges[v].size(); i++)
         {
             // checking for the optimal distance
             if (dist[edges[v][i].to] > dist[v] + edges[v][i].weight)
             {
                 dist[edges[v][i].to] = dist[v] + edges[v][i].weight;
  
                 // Put 0 weight edges to front and 1 weight
                 // edges to back so that vertices are processed
                 // in increasing order of weights.
                 if (edges[v][i].weight == 0)
                     Q.push_front(edges[v][i].to);
                 else
                     Q.push_back(edges[v][i].to);
             }
         }
     }
  
     // printing the shortest distances
     for ( int i=0; i<V; i++)
         cout << dist[i] << " " ;
}
  
void addEdge( int u, int v, int wt)
{
    edges[u].push_back({v, wt});
    edges[v].push_back({u, wt});
}
  
// Driver function
int main()
{
     addEdge(0, 1, 0);
     addEdge(0, 7, 1);
     addEdge(1, 7, 1);
     addEdge(1, 2, 1);
     addEdge(2, 3, 0);
     addEdge(2, 5, 0);
     addEdge(2, 8, 1);
     addEdge(3, 4, 1);
     addEdge(3, 5, 1);
     addEdge(4, 5, 1);
     addEdge(5, 6, 1);
     addEdge(6, 7, 1);
     addEdge(7, 8, 1);
     int src = 0; //source node
     zeroOneBFS(src);
     return 0;
}

Java

// Java Program to implement 0-1 BFS
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
  
public class ZeroOneBFS {
     private static class Node {
         int to; // the ending vertex
         int weight; // the weight of the edge
          
         public Node( int to, int wt) {
             this .to = to;
             this .weight = wt;
         }
     }
      
     private static final int numVertex = 9 ;
     private ArrayList<Node>[] edges = new ArrayList[numVertex];
      
     public ZeroOneBFS() {
         for ( int i = 0 ; i < edges.length; i++) {
             edges[i] = new ArrayList<Node>();
         }
     }
      
     public void addEdge( int u, int v, int wt) {
         edges[u].add(edges[u].size(), new Node(v, wt));
         edges[v].add(edges[v].size(), new Node(u, wt));
     }
      
     public void zeroOneBFS( int src) {
  
         // initialize distances from given source
         int [] dist = new int [numVertex];
         for ( int i = 0 ; i < numVertex; i++) {
             dist[i] = Integer.MAX_VALUE;
         }
          
         // double ended queue to do BFS
         Deque<Integer> queue = new ArrayDeque<Integer>();
         dist[src] = 0 ;
         queue.addLast(src);
          
         while (!queue.isEmpty()) {
             int v = queue.removeFirst();
             for ( int i = 0 ; i < edges[v].size(); i++) {
  
                 // checking for optimal distance
                 if (dist[edges[v].get(i).to] > 
                         dist[v] + edges[v].get(i).weight) {
  
                     // update the distance
                     dist[edges[v].get(i).to] =
                           dist[v] + edges[v].get(i).weight;
  
                     // put 0 weight edges to front and 1
                     // weight edges to back so that vertices
                     // are processed in increasing order of weight
                     if (edges[v].get(i).weight == 0 ) {
                         queue.addFirst(edges[v].get(i).to);
                     } else {
                         queue.addLast(edges[v].get(i).to);
                     }
                 }
             }
         }
          
         for ( int i = 0 ; i < dist.length; i++) {
             System.out.print(dist[i] + " " );
         }
     }
      
     public static void main(String[] args) {
         ZeroOneBFS graph = new ZeroOneBFS();
         graph.addEdge( 0 , 1 , 0 );
         graph.addEdge( 0 , 7 , 1 );
         graph.addEdge( 1 , 7 , 1 );
         graph.addEdge( 1 , 2 , 1 );
         graph.addEdge( 2 , 3 , 0 );
         graph.addEdge( 2 , 5 , 0 );
         graph.addEdge( 2 , 8 , 1 );
         graph.addEdge( 3 , 4 , 1 );
         graph.addEdge( 3 , 5 , 1 );
         graph.addEdge( 4 , 5 , 1 );
         graph.addEdge( 5 , 6 , 1 );
         graph.addEdge( 6 , 7 , 1 );
         graph.addEdge( 7 , 8 , 1 );
         int src = 0 ; //source node
         graph.zeroOneBFS(src);
         return ;
     }
}

Python3

# Python3 program to implement single source
# shortest path for a Binary Graph
from sys import maxsize as INT_MAX
from collections import deque
  
# no.of vertices
V = 9
  
# a structure to represent edges
class node:
     def __init__( self , to, weight):
  
         # two variable one denote the node
         # and other the weight
         self .to = to
         self .weight = weight
  
# vector to store edges
edges = [ 0 ] * V
for i in range (V):
     edges[i] = []
  
# Prints shortest distance from 
# given source to every other vertex
def zeroOneBFS(src: int ):
  
     # Initialize distances from given source
     dist = [ 0 ] * V
     for i in range (V):
         dist[i] = INT_MAX
  
     # double ende queue to do BFS.
     Q = deque()
     dist[src] = 0
     Q.append(src)
  
     while Q:
         v = Q[ 0 ]
         Q.popleft()
  
         for i in range ( len (edges[v])):
  
             # checking for the optimal distance
             if (dist[edges[v][i].to] > 
                 dist[v] + edges[v][i].weight):
                 dist[edges[v][i].to] = dist[v] + edges[v][i].weight
  
                 # Put 0 weight edges to front and 1 weight
                 # edges to back so that vertices are processed
                 # in increasing order of weights.
                 if edges[v][i].weight = = 0 :
                     Q.appendleft(edges[v][i].to)
                 else :
                     Q.append(edges[v][i].to)
  
     # printing the shortest distances
     for i in range (V):
         print (dist[i], end = " " )
     print ()
  
def addEdge(u: int , v: int , wt: int ):
     edges[u].append(node(v, wt))
     edges[u].append(node(v, wt))
  
# Driver Code
if __name__ = = "__main__" :
  
     addEdge( 0 , 1 , 0 )
     addEdge( 0 , 7 , 1 )
     addEdge( 1 , 7 , 1 )
     addEdge( 1 , 2 , 1 )
     addEdge( 2 , 3 , 0 )
     addEdge( 2 , 5 , 0 )
     addEdge( 2 , 8 , 1 )
     addEdge( 3 , 4 , 1 )
     addEdge( 3 , 5 , 1 )
     addEdge( 4 , 5 , 1 )
     addEdge( 5 , 6 , 1 )
     addEdge( 6 , 7 , 1 )
     addEdge( 7 , 8 , 1 )
  
     # source node
     src = 0
     zeroOneBFS(src)
  
# This code is contributed by
# sanjeev2552

输出如下：