二维测量主要处理周长和面积问题。形状是二维的, 例如三角形, 正方形, 矩形, 圆形, 平行四边形等。本主题没有太多变化, 并且大多数问题都基于某些固定公式。
- 周长:2D图形的边界长度称为周长。
- 面积:2D图形包围的区域称为面积。
- 毕达哥拉斯定理:在一个直角三角形中, (斜边)2=(基础)2+(高度)2
三角形
令三角形的三个边为a, b和c。
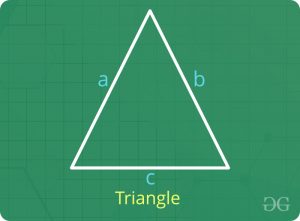
周长= a + b + c
区
2s = a + b + c
面积=
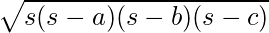
面积= 0.5 x基础x垂直高度
长方形
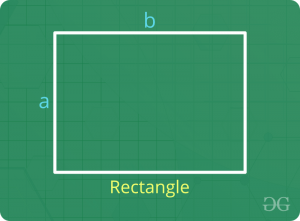
- 周长= 2 x(长度+宽度)
- 面积=长度x宽度
广场
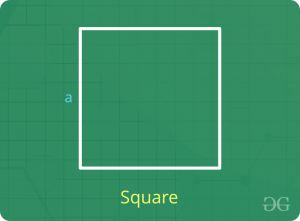
- 周长= 4 x边长
- 面积=(边长)2= 0.5 x(对角线长度)2
平行四边形
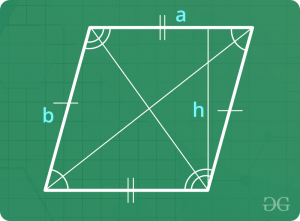
- 周长= 2 x相邻边的总和
- 面积=基础x垂直高度
菱形
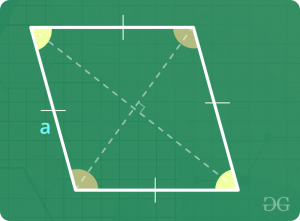
- 周长= 4 x边长
- 面积= 0.5 x对角线乘积
梯形
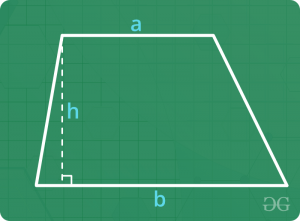
- 周长=各边之和
- 面积= 0.5 x平行边的总和x垂直高度
圈
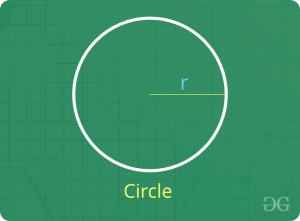
- 周长= 2π半径
- 面积=π(半径)2
- 在圆心对角为θ的弧长=(πx半径xθ)/ 180
- 在圆心处对角为θ的扇形的面积=(πx半径2xθ)/ 360
样本问题
问题1:
求出等边三角形(等边为5厘米, 高度为4厘米)的周长和面积。
解决方案:
应用毕达哥拉斯定理,
(斜边)
2
=(基础)
2
+(高度)
2
=>(5)
2
=(0.5 x等腰三角形的底数)
2
+(4)
2
=> 0.5 x等腰三角形的底边= 3
=>等腰三角形的底部= 6厘米
因此, 周长=所有边的总和= 5 + 5 + 6 = 16厘米
三角形的面积= 0.5 x基础x高度= 0.5 x 6 x 4 = 12厘米
2
问题2 :
使用尺寸为22 cm x 7 cm的矩形块制作可能的最大半径的圆。找到这样形成的圆的面积。
解决方案:
在这样的问题中, 圆的直径的长度和宽度较小。
在这里, 圆的直径= 7厘米
=>圆的半径= 3.5厘米
因此, 圆的面积=π(半径)
2
=π(3.5)
2
= 38.50厘米
2
问题3:
披萨将分成8个相同的部分。每个零件在圆心对着的角度是多少?
解决方案:
用相同的块表示每个块的面积相同。
=>每块面积=(πx半径
2
xθ)/ 360 =(1/8)x圆形披萨的面积
=>(πx半径
2
xθ)/ 360 =(1/8)x(πx半径
2
)
=>θ/ 360 = 1/8
=>θ= 360/8 = 45
因此, 每个零件在圆心处的对角= 45度
问题4:
将四头母牛绑在边长7厘米的正方形区域的每个角上。奶牛用绳子捆起来, 这样每头奶牛都吃草了最大可能的田地, 所有奶牛都吃了相等的面积。找到未平整区域的区域。
解决方案:
为了最大程度地放牧, 每条绳索的长度必须为3.5厘米。
=> 1头牛放牧的面积=(πx半径
2
xθ)/ 360
=> 1头牛放牧的面积=(πx 3.5
2
x 90)/ 360 =(πx 3.5
2
)/ 4
=> 4头牛放牧的面积= 4 x [(πx 3.5
2
)/ 4] =πx 3.5
2
=> 4头牛放牧的面积= 38.5厘米
2
现在, 正方形区域的面积=侧面
2
= 7
2
= 49厘米
2
=>未脱毛面积=耕地面积– 4头牛放牧的面积
=>未擦拭区域= 49 – 38.5 = 10.5厘米
2
问题5:
找到可以刻在半径为" r"的圆中的最大正方形的面积。
解决方案:
可以在圆内切出的最大正方形将以圆的直径作为正方形的对角线。
=>正方形的对角线= 2 r
=>正方形的边= 2 r / 2
1/2
=>正方形的侧面= 2
1/2
[R
因此, 正方形的面积=侧面
2
= [2
1/2
r]
2
= 2 r
2
问题6:
承包商负责围栏长100 m, 宽50 m的矩形区域。围栏的费用为卢比。 2每米, 人工费为Re。每米1美元, 均直接支付给承包商。如果向承包商支付的费用的10%作为税款支付给土地管理局, 则计算围栏的总成本。
解决方案:
每米围栏的总成本= Rs。 2 +1 =卢比。 3
所需的围栏长度=矩形区域的周长= 2(长度+宽度)
=>需要的栅栏长度= 2 x(100 + 50)= 300米
=>支付给承包商的金额= Rs。 3 x 300 = 900
=>支付给土地管理局的金额= 10卢比。 900 =卢比。 90
因此, 围栏的总成本= Rs。 900 + 90 =卢比。 990
关于二维测量的问题套装2
三角形程序
- 查找三角形的面积
- 查找三角形的周长
- 如果给出两个相邻边的两个向量, 则找到三角形的面积
- 计算等边三角形的面积和周长
- 给定底面和面积的三角形的最小高度
矩形程序
- 矩形面积和周长程序
- 两个重叠矩形的总面积
- 在给定周长下可能的矩形最大面积
- 通过从数组中选取四个边来最大面积矩形
- 用给定的坐标找到矩形的最小面积
广场节目
- 程序寻找广场面积
- 对角线长度的正方形面积
- 矩形内所有可能的正方形的面积总和
- 查找正方形和矩形的周长/周长
平行四边形程序
- 平行四边形程序
- 程序查找平行四边形的面积
- 如果给出两个相邻边的向量, 则求出平行四边形的面积
菱形和梯形的程序
- 计算给定对角线的菱形的面积和周长的程序
- 可以刻在矩形中的最大菱形区域
- 梯形的面积和周长的计算程序
循环程序
- 程序寻找一个圆的区域
- 查找圆周的程序
- 程序计算一个正方形内切圆的面积
- 菱形内刻圆的面积
- 正方形的外接圆的面积
- 刻在正六边形上的圆的面积
- 程序来找到三角形的内圆的半径
本文的贡献者:
Nishant Arora
如果你对以上讨论的主题有任何疑问, 或者在任何问题上都遇到困难, 或者你想讨论除上述问题之外的其他问题, 请写评论。
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

