3D测量法处理诸如立方体, 长方体, 球形等形状。问题通常基于体积和表面积。
长方体
假设长方体的长度, 宽度和高度分别为" L", " B"和" H"。
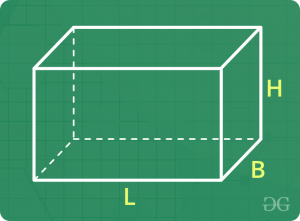
- 体积= L xB x H
- 曲面面积= 2 H(L + B)
- 总表面积= 2(L B + B H + H L)
- 对角线长度=(L2+ B2+ H2)1/2
立方体
令立方体的侧面为" a"
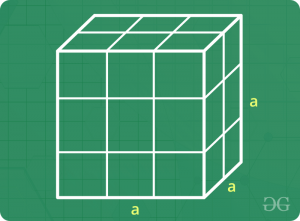
体积= a3
曲面面积= 4 a2
总表面积= 6 a2
对角线长度=
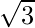
一种
气缸(右圆气缸)
令右圆柱的底边半径和高度分别为" R"和" H"。
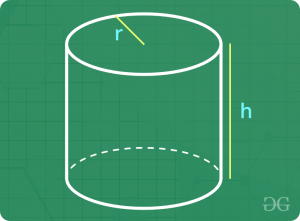
- 体积=πR2H
- 曲面面积= 2πR H
- 总表面积= 2πR H + 2πR2
空心圆柱(空心右圆圆柱)
假设底座的内半径, 底座的外半径和中空右圆柱的高度分别为" r", " R"和" H"。
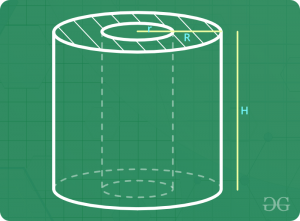
- 体积=πH(R2– r2)
- 曲面面积= 2πR H + 2πr H = 2πH(R + r)
- 总表面积= 2πH(R + r)+ 2π(R2– r2)
锥体
假设底部的半径, 倾斜高度和圆锥体的高度分别为" R", " L"和" H"。
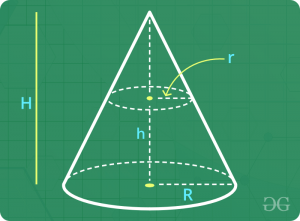
- 大号2= R2+ H2
- 体积=πR2高/ 3
- 弯曲表面积=πR L
- 总表面积=πR L +πR2
领域
假设球体的半径为" R"
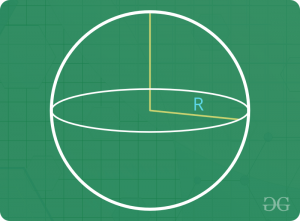
- 体积=(4/3)πR3
- 表面积= 4πR2
半球
假设半球的半径为" R"
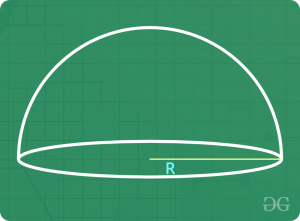
- 体积=(2/3)πR3
- 曲面面积= 2πR2
- 总表面积= 3πR2
请注意, 每当提及"表面面积"时, 我们都会计算总表面积。
样本问题
问题1:
找到可以放在尺寸为10 x 15 x 6 m的立方形房间中的最大杆的长度。
解决方案:
最大的杆将沿着对角线放置。
=>最大杆的长度=房间对角线的长度=(L
2
+ B
2
+ H
2
)
1/2
=>最大杆的长度=(10
2
+ 15
2
+ 6
2
)
1/2
=(100 + 225 + 36)
1/2
=(361)
1/2
=>最大杆的长度= 19 m
问题2 :
找到建造24 m长, 8 m高和60 cm厚的墙所需的尺寸为24 x 12 x 8 cm的砖的数量。
解决方案:
1块砖的体积= 24 x 12 x 8 = 2304厘米
3
墙体体积= 2400 x 800 x 60 = 115200000 cm
3
因此, 所需的砖数= 115200000/2304 = 50000
问题3:
沿着长边滚动一张22厘米x 7厘米的矩形纸, 制成圆柱体。找到所形成的圆柱体的体积。
解决方案:
令圆柱的半径为" R"。
纸张沿着较长的一面滚动。
=> 2πR = 22
=> R = 3.5厘米
另外, 高度= 7厘米
因此, 圆柱体的体积=πR
2
高=π(3.5)
2
7 = 269.5厘米
3
问题4:
如果立方体的每个边缘增加10%, 体积的增加百分比是多少?
解决方案:
假设原始边长为" a"
=>原始体积= a
3
现在, 新的边长= 1.1 a
=>新体积=(1.1 a)
3
= 1.331一个
3
=>体积增加= 1.331 a
3
– 1 a
3
= 0.331 a
3
因此, 体积的百分比增加=(0.331 a
3
/ 一种
3
)x 100 = 33.1%
问题5:
熔化三个边长分别为3 cm, 4 cm, 5 cm的金属立方体, 以形成单个立方体。找到这样的立方体的边缘长度。
解决方案:
新立方体的体积=熔化立方体时产生的金属体积=三个立方体的体积总和
=>新立方体的体积= 3
3
+ 4
3
+ 5
3
= 216
=>新立方体的边长=(216)
1/3
= 6厘米
问题6:
找到制造半径7 m, 高度24 m的圆锥形机器所需的1.25 m宽的金属板的长度。
解决方案:
片材将成形为圆锥形。
=>板材面积=圆锥机面积
=> 1.25 x长度=πx R x L
=> 1.25 x长度=πx R x(7
2
+ 24
2
)
1/2
=> 1.25 x长度=πx 7 x 25
=>长度= 440 m
因此, 需要440 m长的金属板来制造圆锥机。
问题7:
从底部的半径为7厘米, 高度为6厘米的圆柱形容器中, 将水倒入每个半径为3.5厘米的小半球形碗中。确定清空圆柱形容器所需的最小碗数。
解决方案:
圆柱容器的体积=πR
2
高=π(7
2
)6 = 924厘米
3
每个碗的体积=(2/3)πR
3
=(2/3)π3.5
3
= 269.5 / 3
=>所需碗数=(924)/(269.5 / 3)= 10.28
但是由于碗的数量不能零碎, 因此我们需要至少11个这样的碗来清空圆柱形容器。
有关3D测量的问题|套装2
本文的贡献者:
Nishant Arora
如果你对以上讨论的主题有任何疑问, 或者在任何问题上都遇到困难, 或者你想讨论除上述问题之外的其他问题, 请写评论。
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

