模式搜索S6（有限自动机的有效构造）介绍和代码实现

2021年3月13日15:48:09 发表评论 867 次浏览

本文概述

在里面以前的帖子, 我们讨论了基于有限自动机的模式搜索算法。前一篇文章中讨论的FA(有限自动机)构造方法花费O((m ^ 3)* NO_OF_CHARS)时间。可以在O(m * NO_OF_CHARS)时间内构造FA。在这篇文章中, 我们将讨论用于FA构造的O(m * NO_OF_CHARS)算法。这个想法类似于lps(最长前缀后缀)数组的构造, KMP算法。我们使用先前填充的行来填充新行。

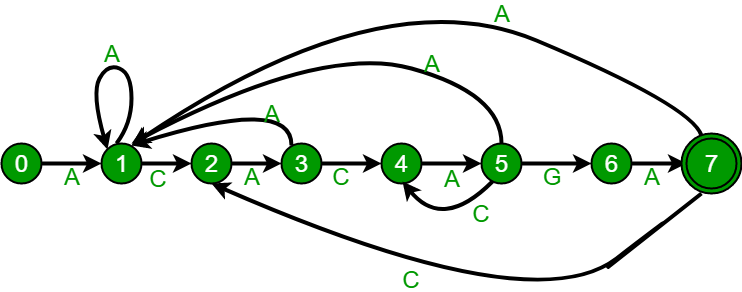
模式搜索第六套（有限自动机的有效构造）1
模式搜索第六套（有限自动机的有效构造）2

上面的图代表ACACAGA模式的图形和表格表示。

算法：

1)填写第一行。除pat [0]字符的条目外, 第一行中的所有条目始终为0。对于pat [0]字符, 我们总是需要进入状态1。

2)将lps初始化为0。第一个索引的lps始终为0。

3)对索引i = 1到M的行执行以下操作(M是模式的长度)

…..a)从索引等于lps的行中复制条目。

…..b)将pat [i]字符的条目更新为i + 1。

…..c)更新lps" lps = TF [lps] [pat [i]]", 其中TF是正在构建的2D数组。

以下是上述算法的C / C ++实现。

实现

C ++

#include <bits/stdc++.h>
using namespace std;
#define NO_OF_CHARS 256
  
/* This function builds the TF table 
which represents Finite Automata for a 
given pattern */
void computeTransFun( char * pat, int M, int TF[][NO_OF_CHARS])
{
     int i, lps = 0, x;
  
     // Fill entries in first row
     for (x = 0; x < NO_OF_CHARS; x++)
         TF[0][x] = 0;
     TF[0][pat[0]] = 1;
  
     // Fill entries in other rows
     for (i = 1; i <= M; i++) {
         // Copy values from row at index lps
         for (x = 0; x < NO_OF_CHARS; x++)
             TF[i][x] = TF[lps][x];
  
         // Update the entry corresponding to this character
         TF[i][pat[i]] = i + 1;
  
         // Update lps for next row to be filled
         if (i < M)
             lps = TF[lps][pat[i]];
     }
}
  
/* Prints all occurrences of pat in txt */
void search( char pat[], char txt[])
{
     int M = strlen (pat);
     int N = strlen (txt);
  
     int TF[M + 1][NO_OF_CHARS];
  
     computeTransFun(pat, M, TF);
  
     // process text over FA.
     int i, j = 0;
     for (i = 0; i < N; i++) {
         j = TF[j][txt[i]];
         if (j == M) {
             cout << "pattern found at index " << i - M + 1 << endl;
         }
     }
}
  
/* Driver code */
int main()
{
     char txt[] = "GEEKS FOR GEEKS" ;
     char pat[] = "GEEKS" ;
     search(pat, txt);
     return 0;
}
  
// This is code is contributed by rathbhupendra

C

#include <stdio.h>
#include <string.h>
#define NO_OF_CHARS 256
  
/* This function builds the TF table which represents Finite Automata for a
    given pattern  */
void computeTransFun( char * pat, int M, int TF[][NO_OF_CHARS])
{
     int i, lps = 0, x;
  
     // Fill entries in first row
     for (x = 0; x < NO_OF_CHARS; x++)
         TF[0][x] = 0;
     TF[0][pat[0]] = 1;
  
     // Fill entries in other rows
     for (i = 1; i <= M; i++) {
         // Copy values from row at index lps
         for (x = 0; x < NO_OF_CHARS; x++)
             TF[i][x] = TF[lps][x];
  
         // Update the entry corresponding to this character
         TF[i][pat[i]] = i + 1;
  
         // Update lps for next row to be filled
         if (i < M)
             lps = TF[lps][pat[i]];
     }
}
  
/* Prints all occurrences of pat in txt */
void search( char * pat, char * txt)
{
     int M = strlen (pat);
     int N = strlen (txt);
  
     int TF[M + 1][NO_OF_CHARS];
  
     computeTransFun(pat, M, TF);
  
     // process text over FA.
     int i, j = 0;
     for (i = 0; i < N; i++) {
         j = TF[j][txt[i]];
         if (j == M) {
             printf ( "\n pattern found at index %d" , i - M + 1);
         }
     }
}
  
/* Driver program to test above function */
int main()
{
     char * txt = "GEEKS FOR GEEKS" ;
     char * pat = "GEEKS" ;
     search(pat, txt);
     getchar ();
     return 0;
}

Java

/* A Java program to answer queries to check whether 
the substrings are palindrome or not efficiently */
  
class GFG
{
  
     static int NO_OF_CHARS = 256 ;
  
     /* This function builds the TF table 
     which represents Finite Automata for a 
     given pattern */
     static void computeTransFun( char [] pat, int M, int TF[][]) 
     {
         int i, lps = 0 , x;
  
         // Fill entries in first row 
         for (x = 0 ; x < NO_OF_CHARS; x++) 
         {
             TF[ 0 ][x] = 0 ;
         }
         TF[ 0 ][pat[ 0 ]] = 1 ;
  
         // Fill entries in other rows 
         for (i = 1 ; i < M; i++) 
         {
             // Copy values from row at index lps 
             for (x = 0 ; x < NO_OF_CHARS; x++) 
             {
                 TF[i][x] = TF[lps][x];
             }
  
             // Update the entry corresponding to this character 
             TF[i][pat[i]] = i + 1 ;
  
             // Update lps for next row to be filled 
             if (i < M) 
             {
                 lps = TF[lps][pat[i]];
             }
         }
     }
  
     /* Prints all occurrences of pat in txt */
     static void search( char pat[], char txt[])
     {
         int M = pat.length;
         int N = txt.length;
  
         int [][] TF = new int [M + 1 ][NO_OF_CHARS];
  
         computeTransFun(pat, M, TF);
  
         // process text over FA. 
         int i, j = 0 ;
         for (i = 0 ; i < N; i++) 
         {
             j = TF[j][txt[i]];
             if (j == M) 
             {
                 System.out.println( "pattern found at index " + 
                                                 (i - M + 1 ));
             }
         }
     }
  
     /* Driver code */
     public static void main(String[] args) 
     {
         char txt[] = "GEEKS FOR GEEKS" .toCharArray();
         char pat[] = "GEEKS" .toCharArray();
         search(pat, txt);
     }
}
  
// This code is contributed by Princi Singh

C#

/* A C# program to answer queries to check whether 
the substrings are palindrome or not efficiently */
using System;
      
class GFG
{
  
     static int NO_OF_CHARS = 256;
  
     /* This function builds the TF table 
     which represents Finite Automata for a 
     given pattern */
     static void computeTransFun( char [] pat, int M, int [, ]TF) 
     {
         int i, lps = 0, x;
  
         // Fill entries in first row 
         for (x = 0; x < NO_OF_CHARS; x++) 
         {
             TF[0, x] = 0;
         }
         TF[0, pat[0]] = 1;
  
         // Fill entries in other rows 
         for (i = 1; i < M; i++) 
         {
             // Copy values from row at index lps 
             for (x = 0; x < NO_OF_CHARS; x++) 
             {
                 TF[i, x] = TF[lps, x];
             }
  
             // Update the entry corresponding to this character 
             TF[i, pat[i]] = i + 1;
  
             // Update lps for next row to be filled 
             if (i < M) 
             {
                 lps = TF[lps, pat[i]];
             }
         }
     }
  
     /* Prints all occurrences of pat in txt */
     static void search( char []pat, char []txt)
     {
         int M = pat.Length;
         int N = txt.Length;
  
         int [, ] TF = new int [M + 1, NO_OF_CHARS];
  
         computeTransFun(pat, M, TF);
  
         // process text over FA. 
         int i, j = 0;
         for (i = 0; i < N; i++) 
         {
             j = TF[j, txt[i]];
             if (j == M) 
             {
                 Console.WriteLine( "pattern found at index " + 
                                                 (i - M + 1));
             }
         }
     }
  
     /* Driver code */
     public static void Main(String[] args) 
     {
         char []txt = "GEEKS FOR GEEKS" .ToCharArray();
         char []pat = "GEEKS" .ToCharArray();
         search(pat, txt);
     }
}
  
// This code is contributed by Rajput-Ji

输出如下：

pattern found at index 0
 pattern found at index 10

FA构造的时间复杂度为O(M * NO_OF_CHARS)。搜索代码与以前的帖子时间复杂度为O(n)。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: