左偏树/左偏堆实现原理和代码实现指南

2021年3月12日15:04:38 发表评论 889 次浏览

左偏树或左偏堆是使用二叉堆的变体实现的优先队列。每个节点都有一个s值(或等级或距离)到最近的叶子的距离。与二叉堆相反(始终是完整的二叉树), 左偏树可能非常不平衡。

以下是时间复杂度of左偏树/堆.

Function       Complexity              Comparison
1) Get Min:       O(1)      [same as both Binary and Binomial]
2) Delete Min:    O(Log n)  [same as both Binary and Binomial]
3) Insert:        O(Log n)  [O(Log n) in Binary and O(1) in 
                            Binomial and O(Log n) for worst case]                                                                  
4) Merge:         O(Log n)  [O(Log n) in Binomial]

左偏树是具有属性的二叉树：

  1. 普通最小堆性质：键(i)> =键(父(i))
  2. 左侧较重：dist(right(i))<= dist(left(i))。在这里, dist(i)是扩展的二叉树表示中从节点i到叶节点的最短路径上的边数(在此表示中, 空子级被视为外部或叶节点)。到达后代外部节点的最短路径是通过正确的子节点。每个子树也是左偏树, dist(i)= 1 + dist(right(i))。

例子：下面的左手树显示了通过上述过程为每个节点计算的距离。最右边的节点的等级为0, 因为此节点的右边子树为null, 并且其父节点的距离为1 x dist(i)= 1 + dist(right(i))。每个节点都遵循相同的规则, 并计算其s值(或等级)。

lt1

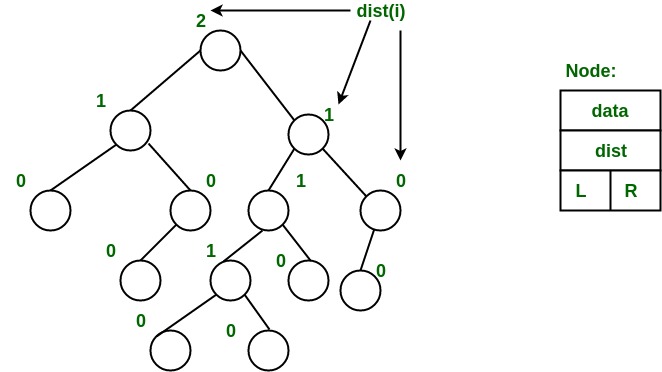
从以上第二个属性, 我们可以得出两个结论：

  1. 从根到最右叶的路径是从根到叶的最短路径。
  2. 如果到最右边的叶子的路径有x个节点, 则左边的堆至少有2个X– 1个节点。这意味着对于具有n个节点的左偏堆, 最右叶的路径长度为O(log n)。

操作方式：

  1. 主要操作是merge()。
  2. deleteMin()(或extractMin())可以通过删除根并为左右子树调用merge()来完成。
  3. 可以通过使用单个键(要插入的键)创建左偏树并为给定树和具有单个节点的树调用merge()来完成insert()。

合并背后的想法：

由于右子树较小, 因此其思想是将一棵树的右子树与其他树合并。以下是抽象步骤。

  1. 将值较小的根作为新根。
  2. 将其左子树挂在左侧。
  3. 递归合并其右子树和另一棵树。
  4. 从递归返回之前：
    –更新合并根目录的dist()。
    –如果需要, 在根目录下交换左右子树, 以保持合并的leftist属性
    结果

资源 ：http://courses.cs.washington.edu/courses/cse326/08sp/lectures/05-leftist-heaps.pdf

合并的详细步骤：

  1. 比较两个堆的根。
  2. 将较小的键推入一个空堆栈, 然后移至较小键的右子项。
  3. 递归比较两个键, 然后继续将较小的键推入堆栈, 然后移至其正确的子级。
  4. 重复直到达到空节点。
  5. 以最后处理的节点为准, 使其成为堆栈顶部节点的右子节点, 如果违反了leftist堆的属性, 则将其转换为leftist堆。
  6. 递归地继续从堆栈中弹出元素, 并使它们成为新堆栈顶部的正确子元素。

例子：

考虑下面给出的两个左偏堆：

2

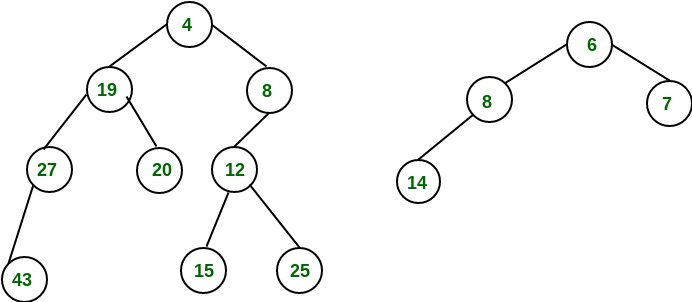
将它们合并为一个左偏堆

3

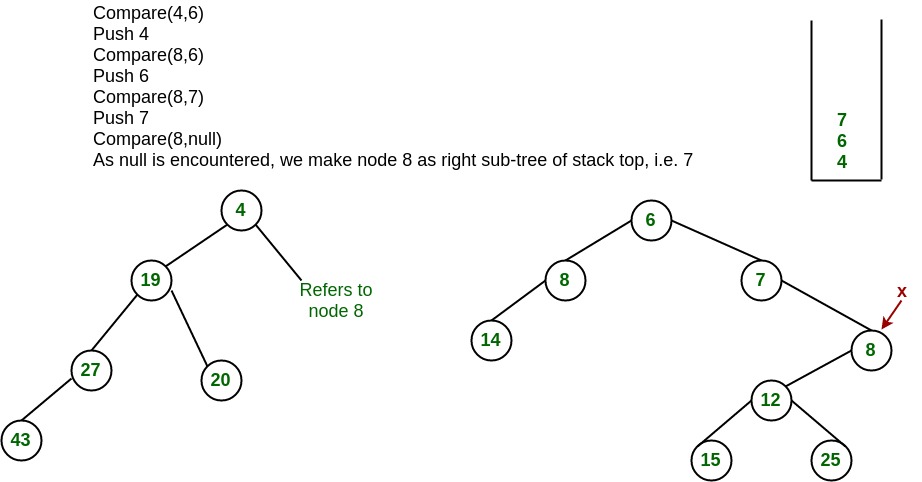
节点7的子树侵犯了左偏堆的属性, 因此我们将其与左子节点交换并保留了左偏堆的属性。

4

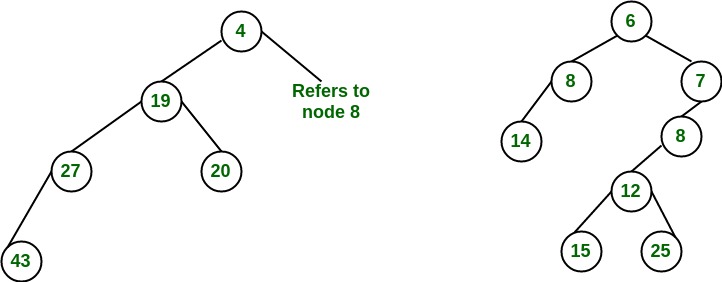
转换为左偏堆。重复这个过程

5
6

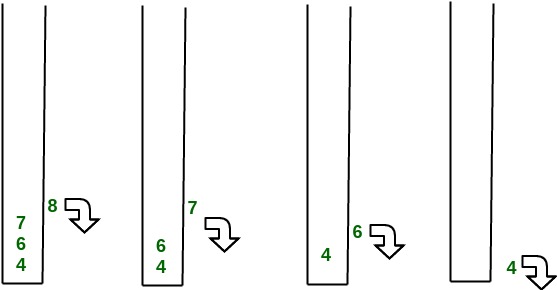
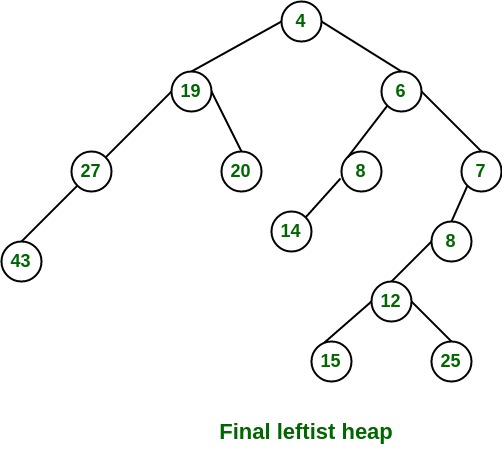
该算法在最坏情况下的时间复杂度在最坏情况下为O(log n), 其中n是左偏堆中的节点数。

合并两个左偏堆的另一个示例：

lt9

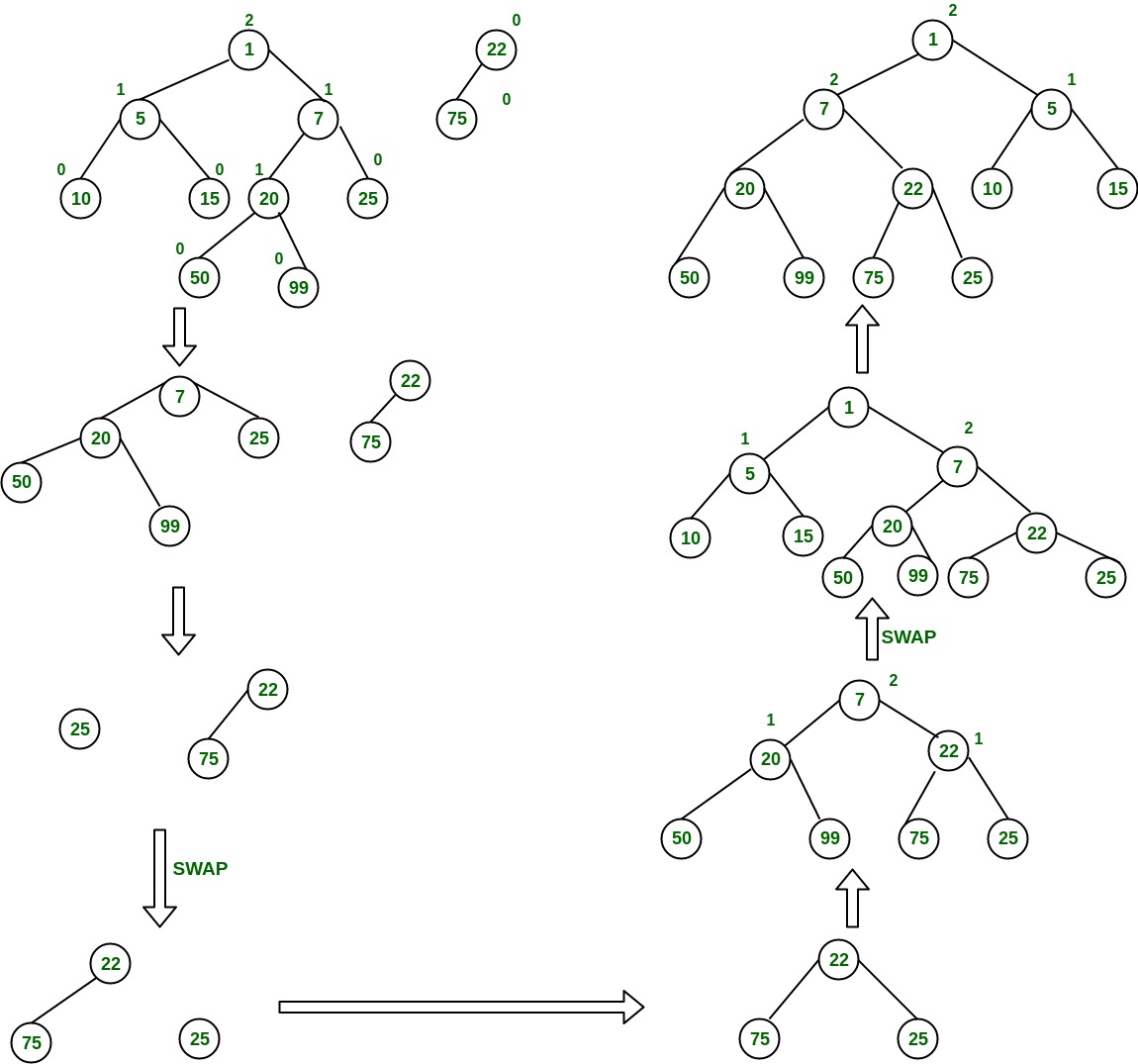
左偏树/左偏堆的实现：

//C++ program for leftist heap / leftist tree
#include <bits/stdc++.h>
using namespace std;
  
// Node Class Declaration
class LeftistNode
{
public :
     int element;
     LeftistNode *left;
     LeftistNode *right;
     int dist;
     LeftistNode( int & element, LeftistNode *lt = NULL, LeftistNode *rt = NULL, int np = 0)
     {
         this ->element = element;
         right = rt;
         left = lt, dist = np;
     }
};
  
//Class Declaration
class LeftistHeap
{
public :
     LeftistHeap();
     LeftistHeap(LeftistHeap &rhs);
     ~LeftistHeap();
     bool isEmpty();
     bool isFull();
     int &findMin();
     void Insert( int &x);
     void deleteMin();
     void deleteMin( int &minItem);
     void makeEmpty();
     void Merge(LeftistHeap &rhs);
     LeftistHeap & operator =(LeftistHeap &rhs);
private :
     LeftistNode *root;
     LeftistNode *Merge(LeftistNode *h1, LeftistNode *h2);
     LeftistNode *Merge1(LeftistNode *h1, LeftistNode *h2);
     void swapChildren(LeftistNode * t);
     void reclaimMemory(LeftistNode * t);
     LeftistNode *clone(LeftistNode *t);
};
  
// Construct the leftist heap
LeftistHeap::LeftistHeap()
{
     root = NULL;
}
  
// Copy constructor.
LeftistHeap::LeftistHeap(LeftistHeap &rhs)
{
     root = NULL;
     * this = rhs;
}
  
// Destruct the leftist heap
LeftistHeap::~LeftistHeap()
{
     makeEmpty( );
}
  
/* Merge rhs into the priority queue.
rhs becomes empty. rhs must be different
from this.*/
void LeftistHeap::Merge(LeftistHeap &rhs)
{
     if ( this == &rhs)
         return ;
     root = Merge(root, rhs.root);
     rhs.root = NULL;
}
  
/* Internal method to merge two roots.
  Deals with deviant cases and calls recursive Merge1.*/
LeftistNode *LeftistHeap::Merge(LeftistNode * h1, LeftistNode * h2)
{
     if (h1 == NULL)
         return h2;
     if (h2 == NULL)
         return h1;
     if (h1->element < h2->element)
         return Merge1(h1, h2);
     else
         return Merge1(h2, h1);
}
  
/* Internal method to merge two roots.
  Assumes trees are not empty, and h1's root contains
   smallest item.*/
LeftistNode *LeftistHeap::Merge1(LeftistNode * h1, LeftistNode * h2)
{
     if (h1->left == NULL)
         h1->left = h2;
     else
     {
         h1->right = Merge(h1->right, h2);
         if (h1->left->dist < h1->right->dist)
             swapChildren(h1);
         h1->dist = h1->right->dist + 1;
     }
     return h1;
}
  
// Swaps t's two children.
void LeftistHeap::swapChildren(LeftistNode * t)
{
     LeftistNode *tmp = t->left;
     t->left = t->right;
     t->right = tmp;
}
  
/* Insert item x into the priority queue, maintaining
   heap order.*/
void LeftistHeap::Insert( int &x)
{
     root = Merge( new LeftistNode(x), root);
}
  
/* Find the smallest item in the priority queue.
Return the smallest item, or throw Underflow if empty.*/
int &LeftistHeap::findMin()
{
     return root->element;
}
  
/* Remove the smallest item from the priority queue.
Throws Underflow if empty.*/
void LeftistHeap::deleteMin()
{
     LeftistNode *oldRoot = root;
     root = Merge(root->left, root->right);
     delete oldRoot;
}
  
/* Remove the smallest item from the priority queue.
Pass back the smallest item, or throw Underflow if empty.*/
void LeftistHeap::deleteMin( int &minItem)
{
     if (isEmpty())
     {
         cout<< "Heap is Empty" <<endl;
         return ;
     }
     minItem = findMin();
     deleteMin();
}
  
/* Test if the priority queue is logically empty.
  Returns true if empty, false otherwise*/
bool LeftistHeap::isEmpty()
{
     return root == NULL;
}
  
/* Test if the priority queue is logically full.
  Returns false in this implementation.*/
bool LeftistHeap::isFull()
{
     return false ;
}
  
// Make the priority queue logically empty
void LeftistHeap::makeEmpty()
{
     reclaimMemory(root);
     root = NULL;
}
  
// Deep copy
LeftistHeap &LeftistHeap::operator =(LeftistHeap & rhs)
{
     if ( this != &rhs)
     {
         makeEmpty();
         root = clone(rhs.root);
     }
     return * this ;
}
  
// Internal method to make the tree empty.
void LeftistHeap::reclaimMemory(LeftistNode * t)
{
     if (t != NULL)
     {
         reclaimMemory(t->left);
         reclaimMemory(t->right);
         delete t;
     }
}
  
// Internal method to clone subtree.
LeftistNode *LeftistHeap::clone(LeftistNode * t)
{
     if (t == NULL)
         return NULL;
     else
         return new LeftistNode(t->element, clone(t->left), clone(t->right), t->dist);
}
  
//Driver program
int main()
{
     LeftistHeap h;
     LeftistHeap h1;
     LeftistHeap h2;
     int x;
     int arr[]= {1, 5, 7, 10, 15};
     int arr1[]= {22, 75};
  
     h.Insert(arr[0]);
     h.Insert(arr[1]);
     h.Insert(arr[2]);
     h.Insert(arr[3]);
     h.Insert(arr[4]);
     h1.Insert(arr1[0]);
     h1.Insert(arr1[1]);
  
     h.deleteMin(x);
     cout<< x <<endl;
  
     h1.deleteMin(x);
     cout<< x <<endl;
  
     h.Merge(h1);
     h2 = h;
  
     h2.deleteMin(x);
     cout<< x << endl;
  
     return 0;
}

输出如下：

1
22
5

参考文献：

维基百科-左偏树

CSC378：左偏树

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: